cs285-lec10-optimal control and planning

Summary

Model-based Reinforcement Leanring

learn the transition probability, then figure out how to choose actions.

Terminology

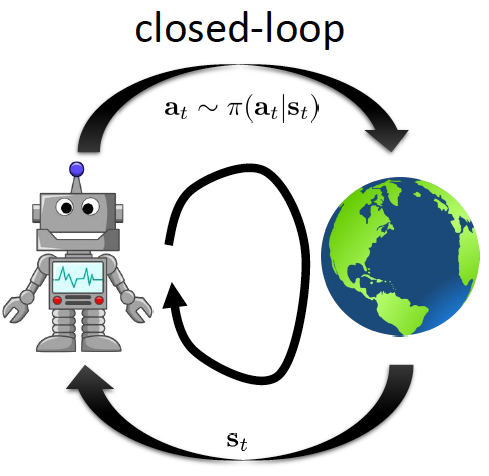
closed-loop: agents take one action per state.

open-loop: agents take all actions once receiving a state.

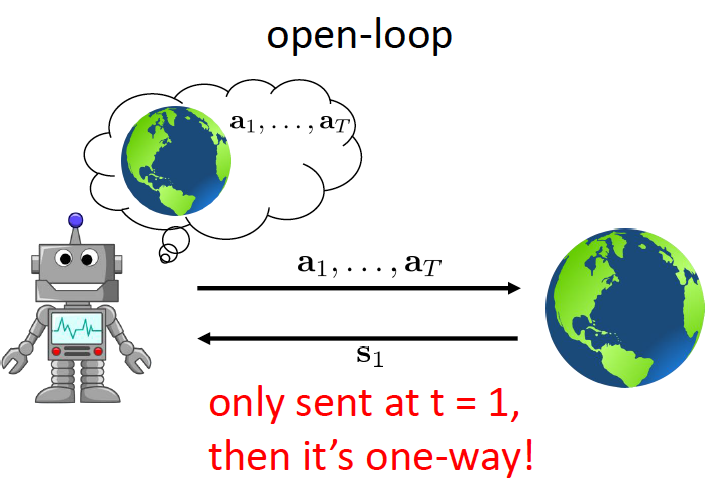
Open-loop Planning

Random Shooting Method

Let’s say $J(A)$ is some method to evaluate the rewards we could get, and $A$ is the action set. Then the objective of optimal planning is:

$A = \argmax_A J(A)$

So the random shooting method is simply guess & check:

1. pick $A_1, A_2, \dots, A_T$ from some distribution (eg: uniform)
2. choose $A_i$ based on $\argmax_iJ(A_i)$

Advantage: efficient (could evaluate $A_i$ in parallel), simple
Disvantage: might not take good actions

Cross-entropy Method (CEM)

Improve the step1 in Random Shooting Method, use better distribution to pick $A$

1. sample $A_1, \dots, A_N$ from $p(A)$
2. evaluate $J(A_1), \dots, J(A_N)$
3. select the elites $A_{i_1}, \dots, A_{i_M}$ that have highest value, where $M < N$
4. refit $p(A)$ to the elites $A_{i_1}, \dots, A_{i_M}$

repeat this process until some condition.

Ususally we use Gaussian Distribution to start.

Advantage & Disadvantage about RSM and CEM

Advantage: fast if run in parallel, and very simple
Disvantage: could only work when dimension is small (no more than 30~60), only work for open-loop planning

Monte Carlo Tree Search (MCTS)

Discreate planning, MCTS runs as follows:

1. find a leaf $s_l$ using TreePolicy($s_1$)
2. evaluate the leaf using DefaultPolicy($s_l$)
3. update all values between $s_1, s_l$

repeat the above process and take the best action from $s_1$

Usually the TreePolicy is UCT TreePolicy: if $s_t$ is not fully expanded, choose new $a_t$, otherwise choose child with best $\text{Score}(s_{t+1})$
We calculate $\text{Score}$ by:

$\text{Score}(s_t) = \underbrace{\frac{Q(s_t)}{N(s_t)}}_{\text{average rewards}} + \underbrace{2C\sqrt{\frac{2\ln N(s_{t-1})}{N(s_t)}}}_{\text{rarely visited nodes}}$

MCTS is used mostly in board games like chess etc.

Trajectory Optimization with Derivatives

TBC