Other Things about DL

Activation Function

Common properties:

Property	Reason
continuous, differentiable*, non-linear	differentiable so we could use back-propagation to learn parameters and optimize loss function
the function and its derivative should be as simple as possible	speed up the calculation
the derivative should fall in a certain range, not too large, not too small	otherwise it would slow down the training speed (TODO: why, ReLU doesn’t obey this)

*Note: Any differentiable function must be continuous at every point in its domain. The converse does not hold: a continuous function need not be differentiable. Eg: $y=|x|$ is continuous, and differentiable everywhere except $x=0$.

sigmoid

Logistic

$\sigma(x) = \frac{1}{ 1 + e^{-x}}$

Property:

1. $\sigma^{'}(x) = \sigma(x) * (1 - \sigma(x))$
2. $\sigma(x) = 1 - \sigma(-x)$

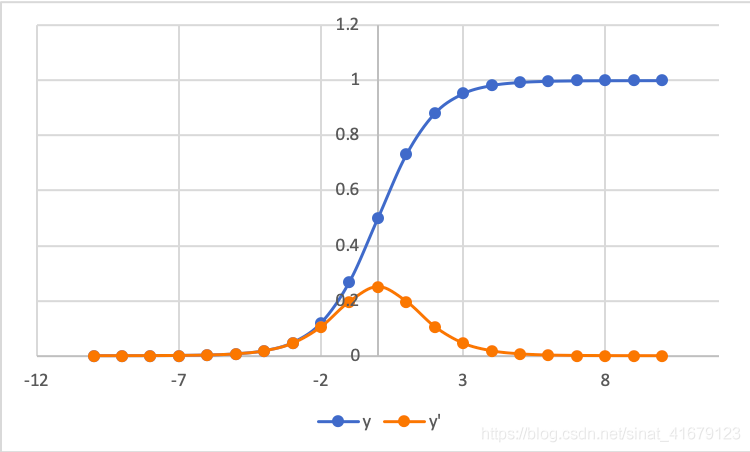Sigmoid and its derivative

For sigmoid function, when $x \in [-3, 3]$, $y=\sigma(x)$ is nearly linear, and $y$ is either 0 or 1 for x outside this range. We call $[-3, 3]$ as a non-saturation regions.

For its first derivative, $\sigma'(x) \approx 0$ when $x \notin [-3, 3]$.

tanh

$tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

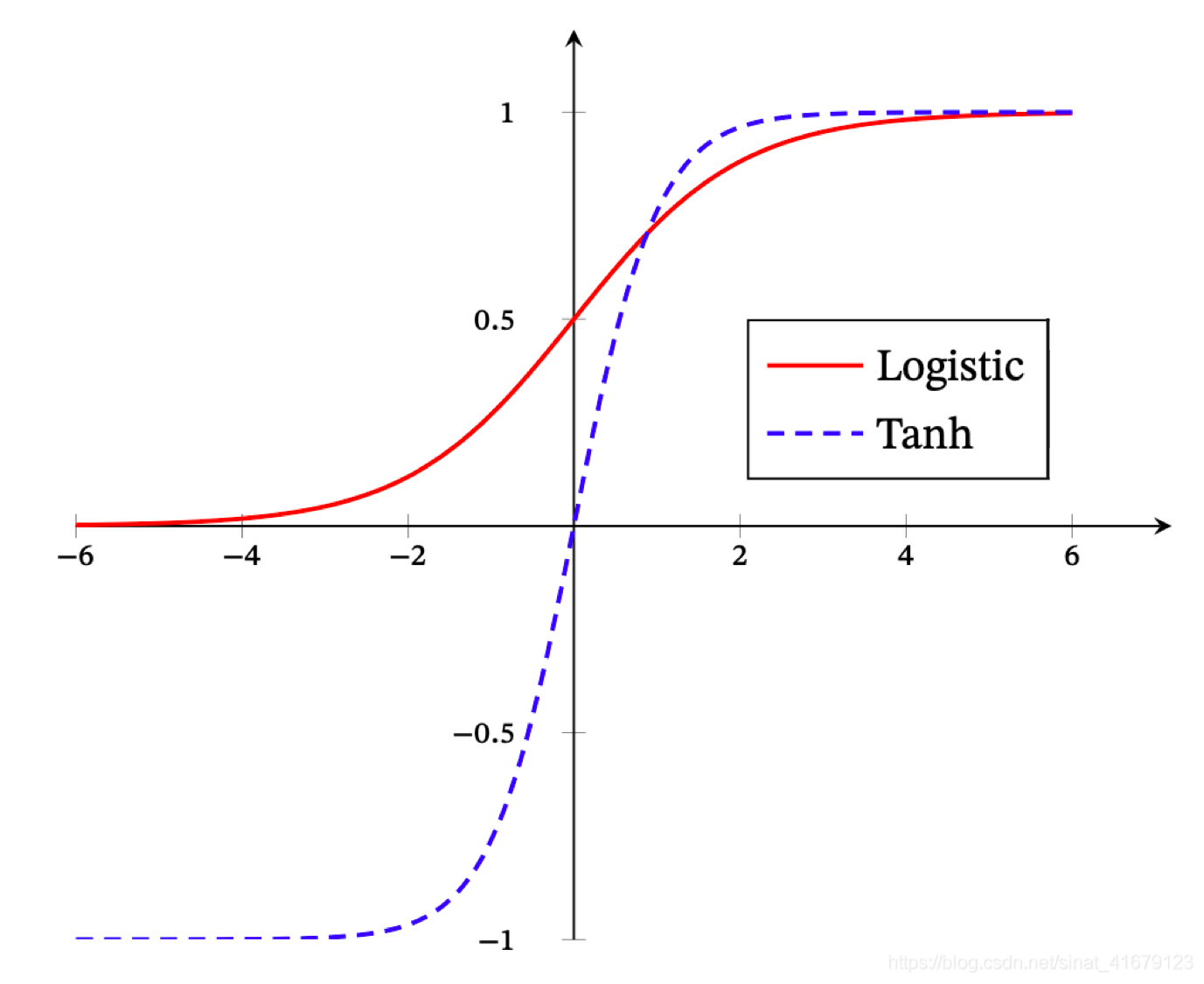tanh and sigmoid

First derivative:
$tanh'(x) = 1 - [tanh(x)]^2$

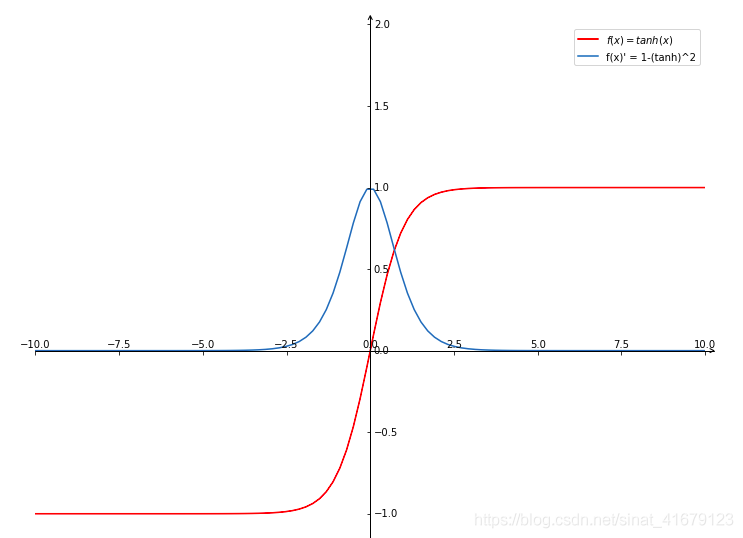tanh and its derivative

@TODO

ReLU/Rectified linear unit

Vanilla ReLU

$relu(x)= \max(0, x) = \begin{cases} x, & x \geq 0 \\ 0 & x < 0 \\ \end{cases}$

Advantages

• Sparse activation: For example, in a randomly initialized network, only about 50% of hidden units are activated (have a non-zero output).
• Better gradient propagation: Fewer vanishing gradient problems compared to sigmoidal activation functions that saturate in both directions.
• Efficient computation: Only comparison, addition and multiplication.
• Scale-invariant: $\max(0, ax)=a\max(0,x), \forall a \geq 0$

Disadvantages

• Non-differentiable at zero: however, it is differentiable anywhere else, and the value of the derivative at zero can be arbitrarily chosen to be 0 or 1.
• Not zero-centered: neurons at later layers would have a position bias.
• Unbounded.
• Dying ReLU problem (vanishing gradient problem): When $x<0$, the derivative of ReLU is 0, meaning the parameter of the neuron won’t udpate by back propagation. And all the neurons that are connected to this neuron won’t update.
  • Possible reasons
    • The initialization of parameters
    • Learning rate is too large. The parameters change too fast from positive to negative.
  • Solutions
    • Leaky ReLU: would reduce performance (TODO:why?)
    • Use auto-scale lr algorithms.

Leaky ReLU

$Leaky \; relu(x)= \begin{cases} x, & x \geq 0 \\ \lambda x & x < 0 \\ \end{cases}$

Parametric ReLU

$P relu_i(x)= \begin{cases} x, & x \geq 0 \\ \lambda_i x & x < 0 \\ \end{cases}$

Where $\lambda_i$ is a learnable parameter.

ELU

Ref: https://nndl.github.io

Softplus

Swish Function

GELU

Maxout

Comparision between different activation functions

TODO

Activation functions developed like this: sigmoid -> tanh -> ReLU -> ReLU variants -> maxout

Activation Function	Advantage	Disvantage
sigmoid	The range of output is $(0,1)$	1. First derivative is nearly 0 at saturation region 2. Not zero-centered, the inputs for later neurons are all positive 3. Slow because of exponential calculation
tanh	Zero-centered, the range of output is $(-1,1)$	1. First derivative is nearly 0 at saturation region 2. Slow because of exponential calculation
ReLU	1. Only 1 saturation region 2. Easy to calculate without exponential	dead ReLU problem
ReLU variants	leaky ReLU, etc. Solved the dead ReLU problem
maxout

Attention Mechanism

Attention works as a weighted sum/avg, the attention score is the weights of every input.

Let’s say inputs are X, here’s how self KV-attention works:

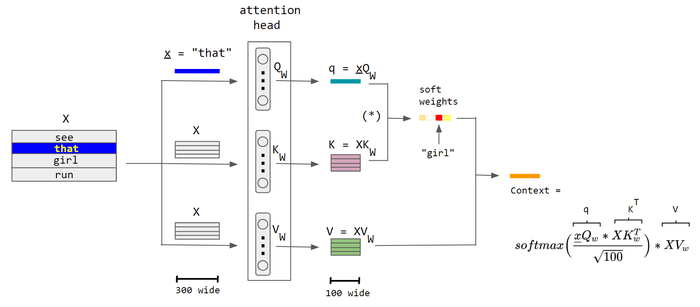KV Attention

The output is:

$O(X) = \sum_{i=1}^n\alpha_iv_i$

where $\alpha_i$ is the attention score of $x_i$, in KV attention, it’s calculated by:

$\alpha_i = f(K, Q)$

Some common ways to calculate attention:

• Standard Scaled Dot-Product Attention

$\text{Attention}(Q,K,V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})*V$

• Multi-Head Attention

$\text{MultiHead}(Q,K,V) = \text{Concat}(\text{head}_1, \text{head}_2, ...)W$

where each head was calculates as:

$\text{head}_i=\text{Attention}(Q,K,V)$

Positional Embedding

Instead of using LSTM/GRU, use positional embedding to capture the positions, usually appears in transformers.

Suppose we have an input sequence with length L, then the positional embedding will be:

$\begin{aligned} P(k, 2i) &= \sin(\frac{k}{n^{2i/d}}) \\ P(k, 2i + 1) &= \cos(\frac{k}{n^{2i/d}}) \\ \end{aligned}$

Where:

1. k is the index of position
2. d is the dimension of positional embedding
3. i is used for mapping column indices
4. n is user-defined number, 10,000 in attention is all you need.

Below is an example:

Example for positional embedding

In transformer, the author added the positional embedding with word embedding, and then feed it into transformer encoder.

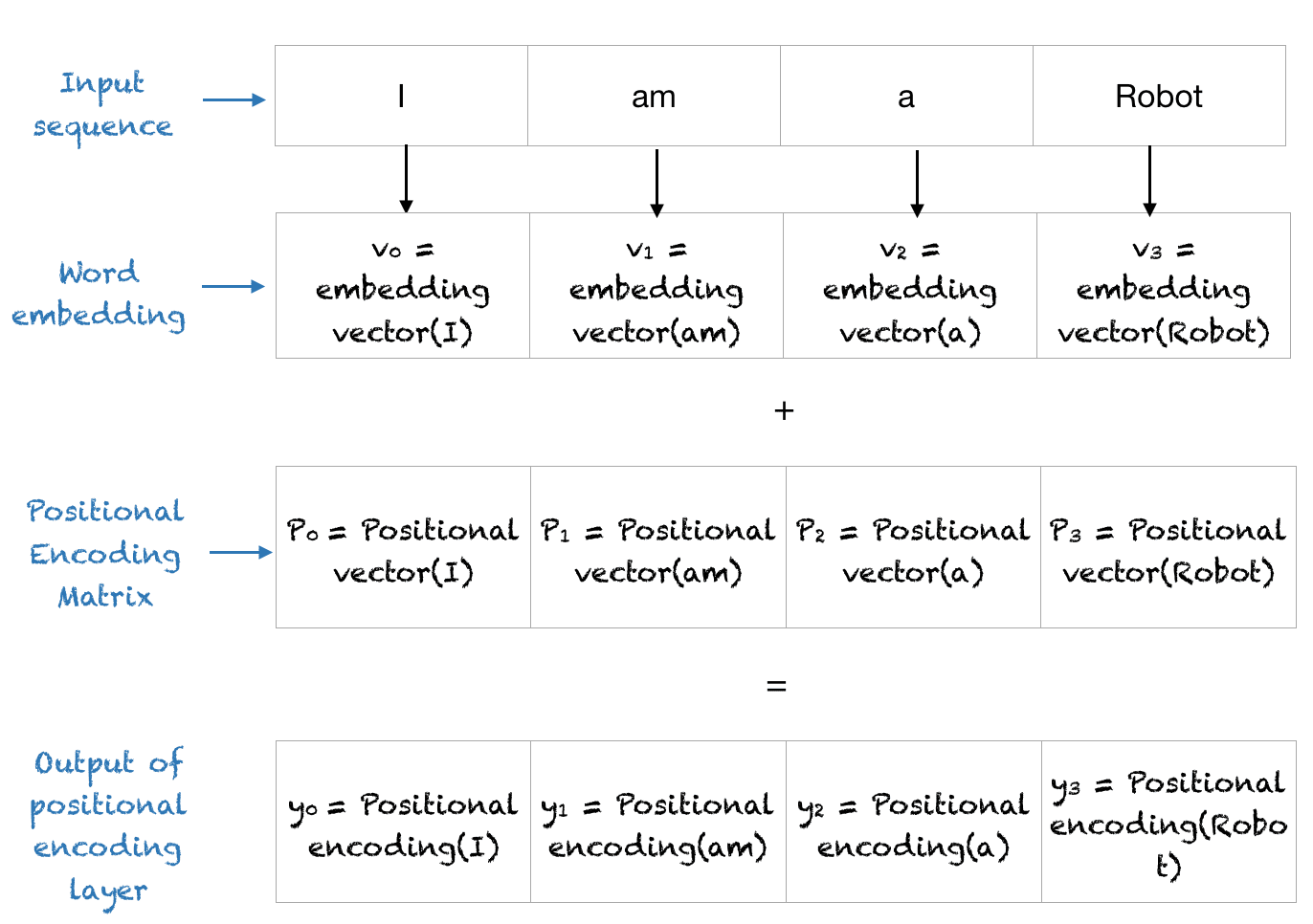How positional embedding works in transformer

Implementation of positional embedding

import numpy as np
import matplotlib.pyplot as plt
 
def getPositionEncoding(seq_len, d, n=10000):
    P = np.zeros((seq_len, d))
    for k in range(seq_len):
        for i in np.arange(int(d/2)):
            denominator = np.power(n, 2*i/d)
            P[k, 2*i] = np.sin(k/denominator)
            P[k, 2*i+1] = np.cos(k/denominator)
    return P

# P.shape: seq_len * d 
P = getPositionEncoding(seq_len=4, d=4, n=100)

Normalization

Note: I call all kinds of feature scalings as normalization.

Why feature scaling?

1. When model is sensitive to distance. If no scaling, then the model will be heavily impacted by the outliners. Or the model will be impacted by features with large ranges.
2. If dataset contains features that have different ranges, units of measurement, or orders of magnitude.

Do the normalization on training set, and use the statistics from training set to test set

Max-Min Scaling/unity-based normalization

Scaled features to range from [0, 1].

$X' = \frac{X - X_{min}}{X_{max} - X_{min}}$

When $X=X_{min}$, then $X'=0$. On the other hand, when $X=X_{max}$, $X'=1$. So this range will be [0, 1]

It could also generalize to restrict the range of values in the dataset between any arbitrary points $a$ and $b$.

$X' = a + \frac{X - X_{min}}{X_{max} - X_{min}} * (b-a)$

Log Scaling

Usually used when there are long tail problems.

$X' = \log(X)$

Z-score

$X' = \frac{X - \text{mean}(X)}{\text{std}(X)}$

After z-score, the distribution of the data would be normal distribution/bell curve.

Property of normal distribution:

1. $\mu=0$
2. $\sigma=1$

For linear models, because they assume the data distribution is normal, so better do normalization.

Batch Normalization

Why use batch normalization?
Because in deep neural networks, the distribution of data will shift through the layers, which is called internal variance.

So we use BN between layers to mitigate the consequences.

How do we do batch normalizations?

For every mini-batch, calculate the normalization of each feature on every sample. The $\mu$ and $\sigma$ are the mean and the variance of the samples respectively.

To be less restrictive, batch normalization add a scaling factor $\gamma$ and an offset $\beta$, so the result is:

$\begin{aligned} X_{BN} &= \gamma \hat{x} + \beta \\ \hat{x} &= \frac{x - \mu(x)}{\sigma(x)} \end{aligned}$

Limitations

• BN calculates based on the batch, so the batch size needs to be big.
• Not suitable for sequence models.

Layer Normalization

Similar to BN, but do the normalization based on feature scale. The $\mu$ and $\sigma$ are the mean and variance of the features on one sample respectively.

LN is calculating the normalization of the features, it’s scaling different features.

LN is more common in NLP, transformer uses layer normalization.

Regularization

Dropout

Dropout is a layer, it can be applied before input layer or hidden layers.

For input layer, the dropout rate is usually 0.2, which means for every input neuron, there’s 80% chance they will be used.
For hidden layer, the dropout rate is usually 0.5.

In pytorch, the implement is as follows:

import torch.nn as nn


class DemoModel(nn.Module):
    def __init__(self):
        super(DemoModel, self).__init__()
        self.dropout_input = nn.Dropout(0.2)
        self.layer1 = nn.Linear(128, 64)
        self.act1 = nn.ReLU()
        self.dropout1 = nn.Dropout(0.5)
        self.layer2 = nn.Linear(64, 32)
        self.act2 = nn.ReLU()
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = self.dropout_input(x)
        x = self.act1(self.layer1(x))
        x = self.act2(self.layer2(x))
        x = self.sigmoid(x)
        return x

When we do the inference, we don’t use dropout, just multiply the drop probability to every weight.

In pytorch, by model.eval(), it will do this automatically.

Early Stop

Stop running the model when triggered. Some early-stop triggers can be:

• No change in the metric over a given number of epochs.
• An absolute change in the metric.
• A decrease in the performance observed over a given number of epochs.
• Average change in the metrics over a given number of epochs.

Initialize

The initialization of the neural network shouldn’t be 0, or too small, or too large.

Initialize to be zeros
All the neurons will give the same effects to the output, when back propagating, the weights will be the same.

Initialize too small
Gradient vanishing.

initialize too large
Gradient explosion.

The common way to initialize is making sure: $\mu = 0, \sigma=1$, which means it’s like a standard normal distribution.

Also, we want to keep the variance the same accross every layer.

Xavier Initialization

Initialize the weights to have $\mu=0$, and $\sigma$ the same across all layers.

Normal xavier initialization

$W \sim N(0, \sqrt{\frac{2}{n_{input} + n_{output}}})$

where $n_{input}, n_{output}$ are the number of input in the input layer and the number of output in the output layer respectively.

Uniform xavier initialization

$W \sim U(\sqrt{\frac{6}{n_{input} + n_{output}}})$

Xavier works better with tanh and sigmoid activation functions.

For ReLU function, usually we use He initialization.

Questions

Why use $\sigma(x)$ as activation function?

Why ReLU instead of $\sigma(x)$?

not saturate in both directions
allow faster and effective training of deep neural architectures on large and complex datasets.