Fundamental Models in CTR & Recommender System

FM/Factorization Machines

Rendle, S. (2010). Factorization machines. 2010 IEEE International Conference on Data Mining (pp. 995–1000).

Summary

1. Introduced the crossed feature with low computational complexity to be $o(kn)$, where k is the dimension of latent vector, and n is the dimension of original feature
2. Suitable for sparse feature. When feature is sparse, could use smaller k to fit.

Details

Assume we have n features in total, if we need to fit the interaction between 2 features (2-degree), then the model will be:

$\begin{aligned} f(\bold{x}) &= w_0 + \sum_{i = 1}^n w_i x_i + \sum_{i = 1}^n \sum_{j = i + 1}^n w_{ij} x_i x_j \\ \end{aligned}$

Since the number of $x_i x_j$ is $\frac{n (n - 1)}{2}$, the computational complexity of this model is $o(n^2)$.

Because $w_{ij}$ is a symmetric matrix, and accroding to Cholesky decomposition, every symmetric matrix is a product of lower-triangular matrix and its transpose, so we have:

$\bold{W} = \bold{V}^T \bold{V}$

Where $\bold{V}$ is a vector of K dimension, and could be seen as the latent vector.

Now for the model, we have:

$\begin{aligned} f(\bold{x}) &= w_0 + \sum_{i = 1}^n w_i x_i + \sum_{i = 1}^n \sum_{j = i + 1}^n w_{ij} x_i x_j \\ &= w_0 + \sum_{i = 1}^n w_i x_i + \sum_{i = 1}^n \sum_{j = i + 1}^n \vec{v_i} \vec{v_j} x_i x_j \\ \end{aligned}$

And the computational complexity is $o(kn^2)$.

For $x_ix_j$, we could decompose it by:

$\begin{aligned} & (x_1 + x_2 + x_3)^2 = x_1^2 + x_2^2 + x_3^2 + 2x_1x_2 + 2x_1x_3 + 2x_2x_3 \\ \Leftrightarrow & \;\;x_1x_2 + x_1x_3 + x_2x_3 = \frac{(x_1 + x_2 + x_3)^2 - x_1^2 + x_2^2 + x_3^2}{2} \end{aligned}$

So now the model is:

$\begin{aligned} f(x) &= w_0 + \sum_{i = 1}^n w_i x_i + \sum_{i = 1}^n \sum_{j = i + 1}^n \vec{v_i} \vec{v_j} x_i x_j \\ &= w_0 + \sum_{i = 1}^n w_i x_i +\frac{1}{2} [(\sum_{i = 1}^n v_ix_i)^2 - \sum_{i = 1}^nv_i^2x_i^2] \\ \end{aligned}$

And the computational complexity is $o(kn)$

Wide & Deep

https://dl.acm.org/doi/10.1145/2988450.2988454

Summary

Use wide part to fit crossed features, and use deep part to fit embeddings for categorical features.

Details

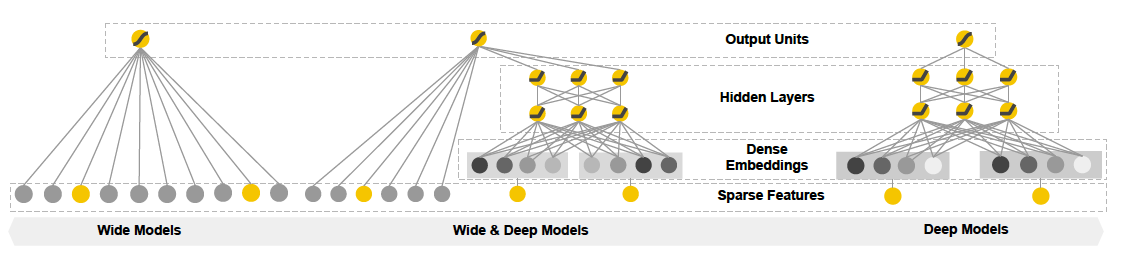Wide & Deep

wide: lr + 2-degree crossed feature, $y_{wide} = w_0 + \sum_i^n{w_ix_i} + \sum_{i = 1}^n{\sum_{j = 1}^n{w_{ij}x_ix_j}}$
deep: dnn, $y_{deep} = DNN(x)$
final: $y = \sigma(y_{wide} + y_{deep} + b)$

It’s used for app recommendation, so a more business graph is as below:

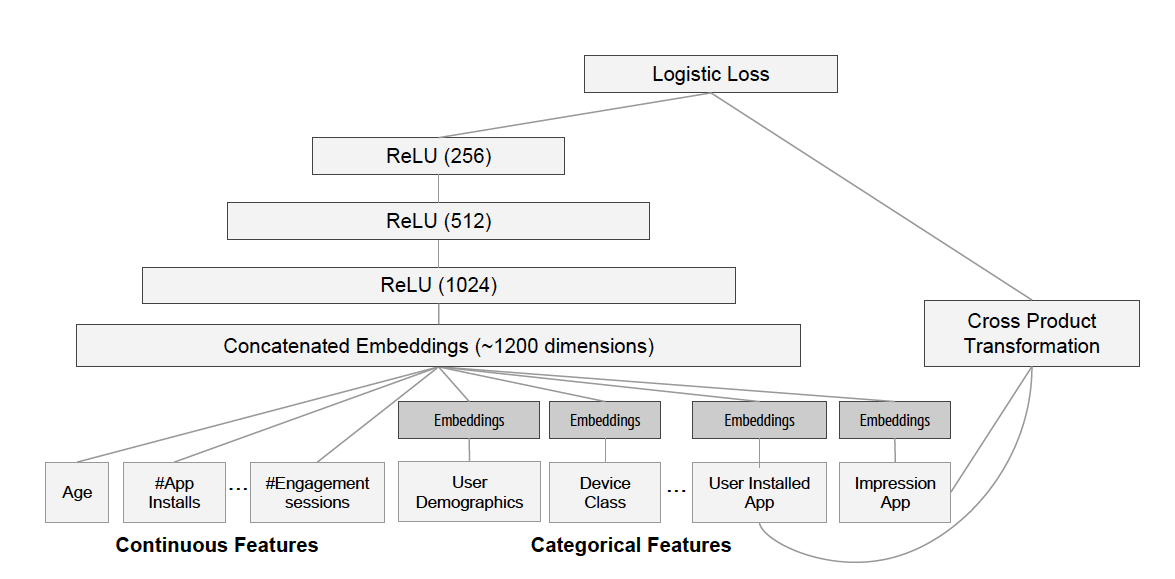Wide & Deep for app recommendation

Here the auther only used user installed app and impression app for crossed features.

what is ReLU(1024)?

Note here, it still requires to choose features for cross features by human, which is diffcult if the number of features is large.

DeepFM

https://arxiv.org/abs/1703.04247

Summary

Use FM to replace wide part in wide & deep, and use embedding for both wide and deep parts.

Details

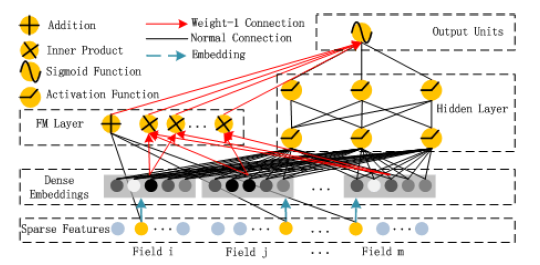DeepFM

Use latent vector from FM as the embedding, to be the input for both deep and wide parts.

DIN/Deep Interest Network for Click-Through Rate Prediction

Summary

Use attention mechanism where:
Query: target ad
Key: User behavior
Value: User behavior
And use an activation network to replace attention score function.

Details

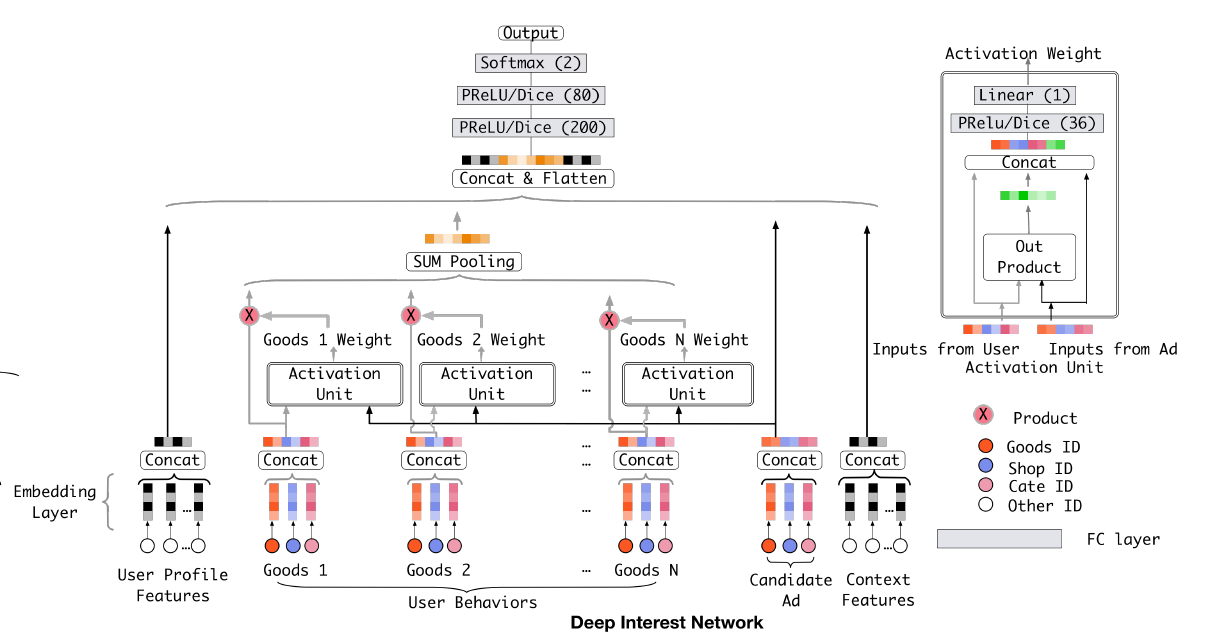DIN

TODO

DIEN/Deep Interest Evolution Network for Click-Through Rate Prediction

Summary

Use GRU to fit user historical behaviour.

Details

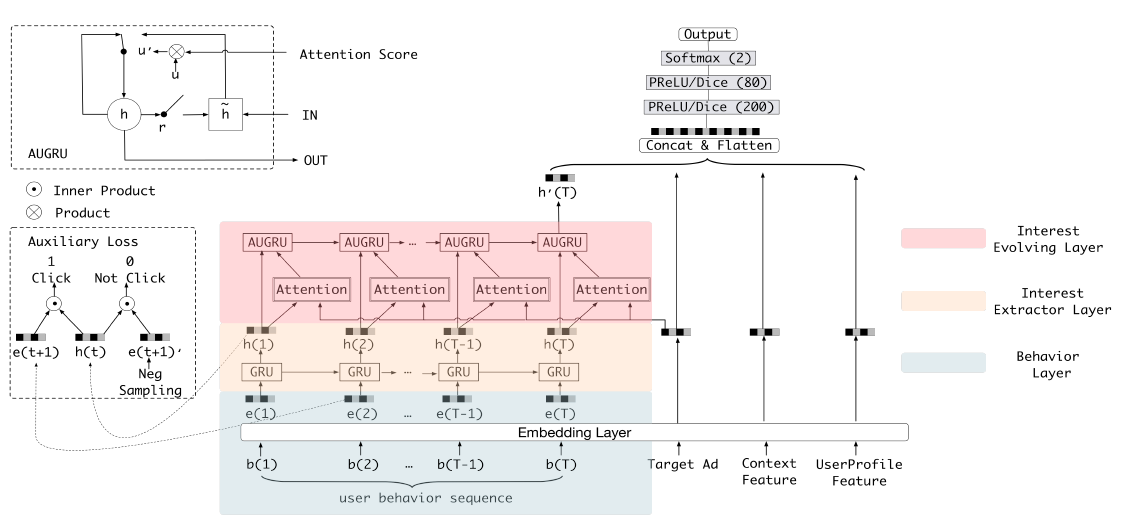DIEN

TODO