Deep Learning Models

Edited on In , Views:

Multilayer perceptron (MLP)/ artificial neural network (ANN) / deep neural network (DNN) / feedforward neural network (FNN)

A neural network is actually a weight matrix, assume we have xx as input, and the output is oo, and we only have 1 hidden layer.
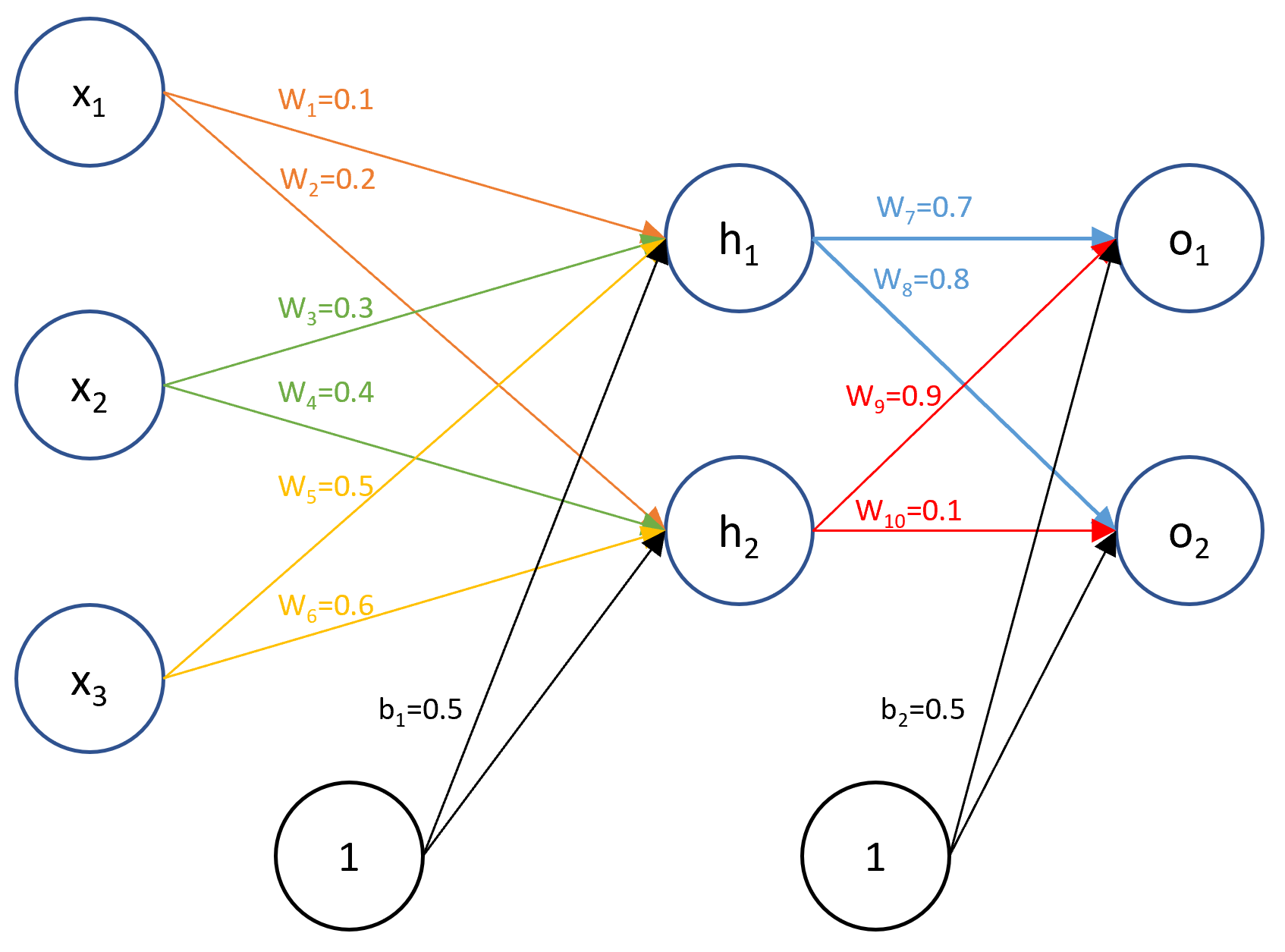Neural Network

The forward function is:

Zl=WlXl−1+blXl−1=fl(Zl−1)\begin{aligned} Z_l &= W^l X_{l-1} + b^l \\ X_{l-1} &= f_l(Z_{l-1}) \end{aligned}

where:

  1. ZlZ_l is the input before activation functions
  2. XlX_l is the output of neurals (after activation)
  3. flf_l is the activation function.

Steps to train the neural network:

  1. Initialize the weights
  2. Forward: Calculate oo with w,bw, b
  3. Back-propagation: Calculate the derivate of loss function
  4. Iterate until loss below certain value

Assume:
x1=1,x2=4,x3=5,y1=0.1,y2=0.05x_1 = 1, x_2 = 4, x_3 = 5, y_1 = 0.1, y_2 = 0.05
Activation function: fl(x)=σ(x)=11+e−xf_l(x) = \sigma(x) = \frac{1}{1 + e^{-x}}
Loss function: L(y^,y)=12∑im(yi^−yi)2L(\hat{y}, y) = \frac{1}{2} \sum_i^m{(\hat{y_i} - y_i)^2}

Use the picture above.

Forward:

Zh1=w1∗x1+w3∗x2+w5∗x3+b1=4.3h1=fl(Zh1)=0.9866Zh2=w2∗x1+w4∗x2+w6∗x3+b2=5.3h2=fl(Zh2)=0.9950Zo1=w7∗h1+w9∗h2+b2=5.3o1=fl(Zo1)=0.8896Zo2=w8∗h1+w10∗h2+b2=1.3888o2=fl(Zo2)=0.8004\begin{aligned} Z_{h1} &= w_1 * x_1 + w_3 * x_2 + w_5 * x_3 + b_1 = 4.3 \\ h_1 &= f_l(Z_{h1}) = 0.9866 \\ Z_{h2} &= w_2 * x_1 + w_4 * x_2 + w_6 * x_3 + b_2 = 5.3 \\ h_2 &= f_l(Z_{h2}) = 0.9950 \\ Z_{o1} &= w_7 * h_1 + w_9 * h_2 + b_2 = 5.3 \\ o_1 &= f_l(Z_{o1}) = 0.8896 \\ Z_{o2} &= w_8 * h_1 + w_10 * h_2 + b_2 = 1.3888 \\ o_2 &= f_l(Z_{o2}) = 0.8004 \\ \end{aligned}

Then o1,o2o_1, o_2 is our predictions for y1,y2y_1, y_2 at the first time. We use back-propagation to optimize:

Back-propagation (only use w1w_1 as an example):

∂L∂w1=∂L∂o1∗∂o1∂w1+∂L∂o2∗∂o2∂w1=∂L∂o1∗∂o1∂zo1∗∂zo1∂w1+∂L∂o2∗∂o2∂zo2∗∂zo2∂w1=∂L∂o1∗∂o1∂zo1∗∂zo1∂h1∗∂h1∂zh1∗∂zh1∂w1+∂L∂o2∗∂o2∂zo2∗∂zo2∂h2∗∂h2∂zh2∗∂zh2∂w2\begin{aligned} \frac{\partial{L}}{\partial{w_1}} &= \frac{\partial{L}}{\partial{o_1}} * \frac{\partial{o_1}}{\partial{w_1}}+ \frac{\partial{L}}{\partial{o_2}} * \frac{\partial{o_2}}{\partial{w_1}} \\ &= \frac{\partial{L}}{\partial{o_1}} * \frac{\partial{o_1}}{\partial{z_{o_1}}} * \frac{\partial{z_{o_1}}}{\partial{w_1}} + \frac{\partial{L}}{\partial{o_2}} * \frac{\partial{o_2}}{\partial{z_{o_2}}} * \frac{\partial{z_{o_2}}}{\partial{w_1}} \\ &= \frac{\partial{L}}{\partial{o_1}} * \frac{\partial{o_1}}{\partial{z_{o_1}}} * \frac{\partial{z_{o_1}}}{\partial{h_1}} * \frac{\partial{h_1}}{\partial{z_{h_1}}} * \frac{\partial{z_{h_1}}}{\partial{w_1}} + \frac{\partial{L}}{\partial{o_2}} * \frac{\partial{o_2}}{\partial{z_{o_2}}} * \frac{\partial{z_{o_2}}}{\partial{h_2}} * \frac{\partial{h_2}}{\partial{z_{h_2}}} * \frac{\partial{z_{h_2}}}{\partial{w_2}} \end{aligned}

From the formula we could see, if the derivate of loss function is less than 1, then after several multiplies the final result would be very small.

Ref: https://www.anotsorandomwalk.com/backpropagation-example-with-numbers-step-by-step/

Gradient Exploding & Gradient Vanishing

Why do we have thus problems?
Back propagation computes the gradient by chain rule. From the back propagation formula, we could see if the number of hidden layers is large, then the result would involve many intermediate gradients. And if the intermediate gradients are below 1, then the products of them would decrease rapidly, thus the gradient would vanish. On the other hand, if the gradients are all above 1, then the product would increase rapidly, so the final gradient would explode.

How to deal with gradient exploding?
To deal with gradient exploding, we can use a gradient clip method. When the gradient is above the threshold, then:

g=∣∣Threshold∣∣∣∣g∣∣∗gg = \frac{||\text{Threshold}||}{||g||}*g

How to deal with gradient vanishing?

  1. Model architecture: use LSTM, GRU.
  2. Residual: Add residual into the network
  3. Batch Normalization: TODO
  4. Activation function: use ReLU instead of sigmoid

Convolutional Neural Network (CNN)

@TODO

Recurrent Neural Network (RNN)

Sometimes the output of the neural network is not only related to input, but also related to current state (output from last time period)

Vanilla RNN
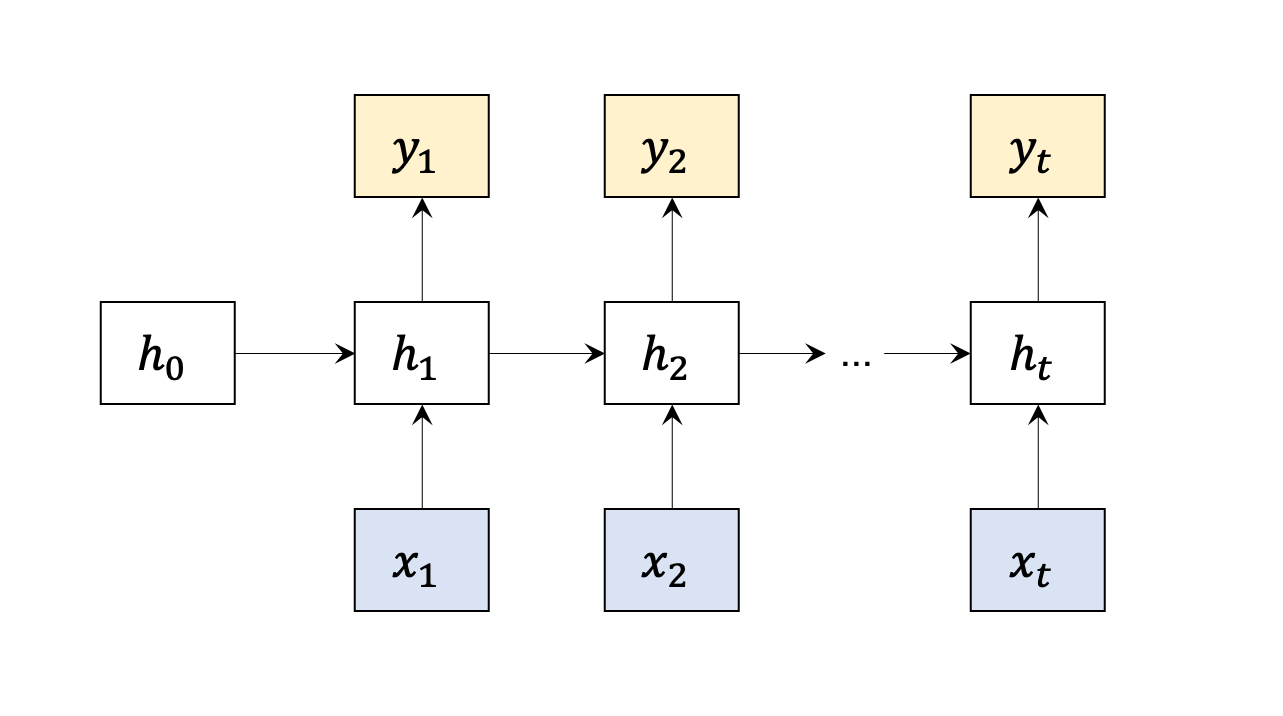vanilla rnn

Forward:

{ht=fh(WxX+Whht−1+bx)yt=fy(Wyht+by) \begin{cases} h_t &= f_h(W_x X + W_h h_{t-1} + b_x) \\ y_t &= f_y(W_yh_t + b_y) \end{cases}

Note: Wx,Wh,WyW_x, W_h, W_y doesn’t change accroding to tt, that’s called weight shareing.

Back-propagation:

∂L∂Wh=∂L∂y1∗∂y1∂wh+∂L∂y2∗∂y2∂wh+⋯+∂L∂yt∗∂yt∂wh\begin{aligned} \frac{\partial{L}}{\partial{W_h}} &= \frac{\partial{L}}{\partial{y_1}} * \frac{\partial{y_1}}{\partial{w_h}}+ \frac{\partial{L}}{\partial{y_2}} * \frac{\partial{y_2}}{\partial{w_h}} + \dots + \frac{\partial{L}}{\partial{y_t}} * \frac{\partial{y_t}}{\partial{w_h}} \end{aligned}

Sometimes to simplify calculation process, we would use a cutoff to shorten the window.

Different Architectures for Different Applications

ref: https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks

Type of RNN Illustration Example
one-to-one, Nx=Ny=1N_x = N_y = 1 Traditional neural network
1-to-many, Nx=1,Ny>1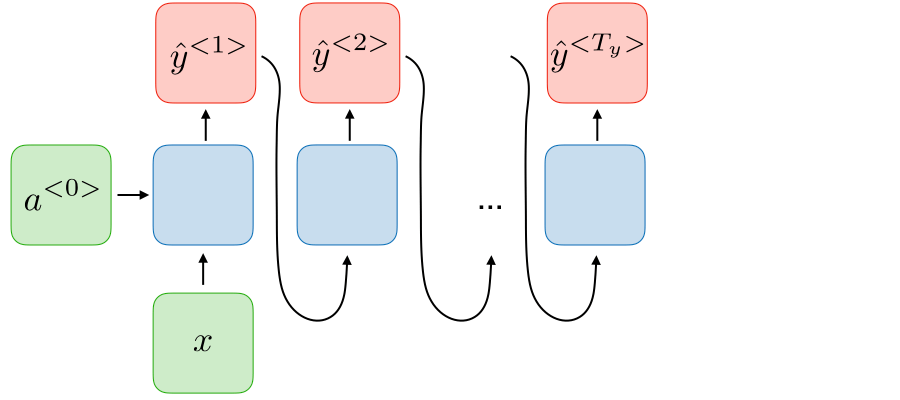N_x = 1, N_y > 1 Music generation
many-to-1, Nx>1,Ny=1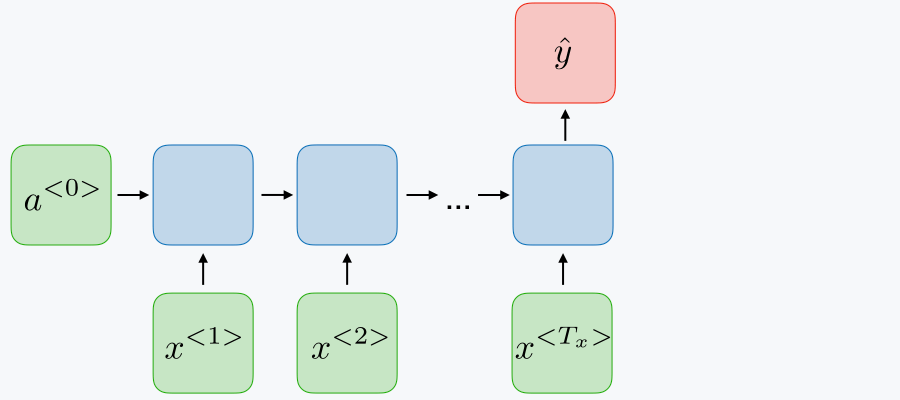N_x > 1, N_y = 1 Sentiment classification
many-to-many, Nx=Ny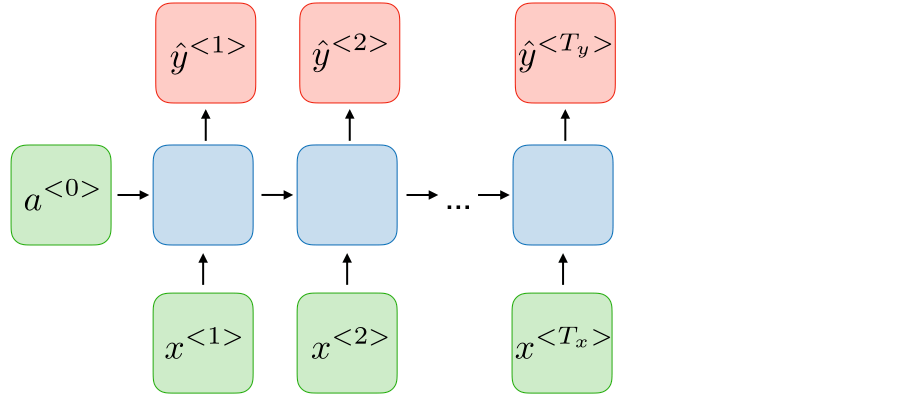N_x = N_y Name entity recognition
many-to-many, Nx≠NyN_x \neq N_y
encoer-decoder
seq2seq		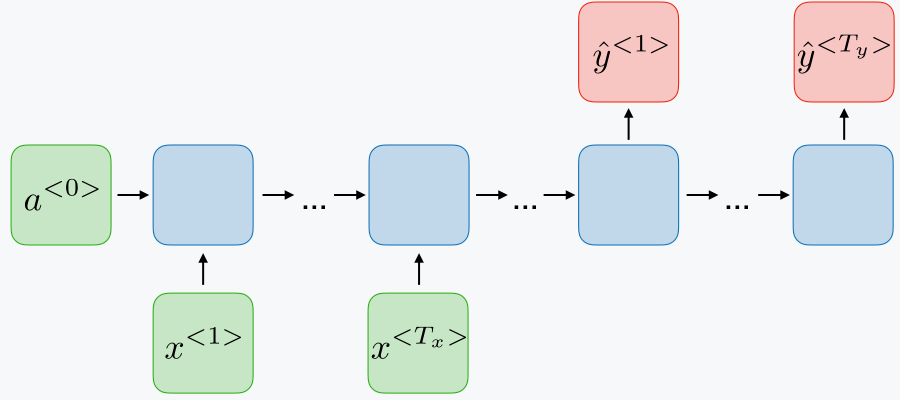 Machine translation

RNN & Gradient Vanishing
For rnn, the gradient vanishing problem is even more severe, because usually the length of sequence is large.

Long Short Term Memory/LSTM

In vanilla RNN, hth_t is changing all the time, and it’s only based on the previous state, like a short memory. So here in LSTM, we introduce a cell ct\boldsymbol{c_t} to use longer memories (long short memory).

To avoid gradient vanishing/gradient exploding problem, LSTM introduce 3 gates: forget gate ft\boldsymbol{f_t}, input/update gate it\boldsymbol{i_t}, output gate ot\boldsymbol{o_t}.

Core idea of LSTM:

  1. Output ht\boldsymbol{h_t} is based on cell ct\boldsymbol{c_t}, that is: ht=ot⊗tanh(ct)\boldsymbol{h_t} = \boldsymbol{o_t} \otimes tanh(\boldsymbol{c_t})
  2. Cell: ct=it⊗tanh(Wc[xt,ht−1]+bc)+ft⊗ct−1\boldsymbol{c_t} = \boldsymbol{i_t} \otimes tanh(W_c[x_t , h_{t - 1}] + b_c) + \boldsymbol{f_t} \otimes \boldsymbol{c_{t-1}}

Where:

  1. ⊗\otimes is the outer product, multiply elementwise
  2. tanh⁡(x)\tanh(x) is the activation function here, because its derivative is larger. Could be replaced with ReLU here.
  3. The gates are also calculated by xt,htx_t, h_t:

ft=σ(Wf[xt,ht−1]+bf)it=σ(Wi[xt,ht−1]+bi)ot=σ(Wo[xt,ht−1]+bo)\begin{aligned} \boldsymbol{f_t} &= \sigma(W_f [x_t, h_{t - 1}] + b_f) \\ \boldsymbol{i_t} &= \sigma(W_i [x_t, h_{t - 1}] + b_i) \\ \boldsymbol{o_t} &= \sigma(W_o [x_t, h_{t - 1}] + b_o) \\ \end{aligned}

here we use σ\sigma because σ\sigma has a value of [0,1][0, 1], which is “gate”.
4. The number of trainable parameters is related to input dimension and hidden layers, which is: (input_dim + hidden_unit + 1) * hidden_unit * 4
Proof: Trainable parameters come from 4 parts: 3 gates and the neural network. Since the inputs of the networks are concatenation of xtx_t and hth_t, the dimension of the concatenated vector is 1 x (input_dim + hidden_unit). And we have 1 dimension for bb, so for one part, the dimension is (input_dim + hidden_unit + 1) x hidden_unit, times 4 we get the final answer.

Gated Recurrent Unit/GRU

In LSTM, we have redundant gates ft\boldsymbol{f_t} and it\boldsymbol{i_t}. So instead of using 3 gates, we only use 2 gates in GRU, reset gate rt\boldsymbol{r_t} and update gate ut\boldsymbol{u_t}.

Output ht\boldsymbol{h_t}:

ht=ut⊗ht−1+(1−ut)⊗tanh(Wc[xt,rt⊗ht−1]+bc)\boldsymbol{h_t} = \boldsymbol{u_t} \otimes h_{t - 1} + (1 - \boldsymbol{u_t}) \otimes tanh(W_c[x_t, \boldsymbol{r_t} \otimes h_{t - 1}] + b_c)

Similar to LSTM, ut\boldsymbol{u_t} and rt\boldsymbol{r_t} are also calculated by ht,xth_t, x_t:

ut=σ(Wu[xt,ht−1]+bu)rt=σ(Wr[xt,ht−1]+br)\begin{aligned} \boldsymbol{u_t} &= \sigma(W_u[x_t, h_{t - 1}] + b_u) \\ \boldsymbol{r_t} &= \sigma(W_r[x_t, h_{t - 1}] + b_r) \\ \end{aligned}