Other Things about ML - 1

Entropy

Entropy

In information theory, entropy is the amount of uncertainty, assume the probability distribution of a single discreate random variable x is $P(x)$, then the entropy of x is:

$H(x) = -\sum_x P(x)\log P(x)$

Note: Entropy cares only the probability distribution of a variable, it has nothing to do with the value of the variable.

Joint Entropy

For 2 discreate random variables $X$ and $Y$, assume the joint probability distribution is $P(x,y)$, then the joint entropy is:

$H(X,Y) = -\sum_{x,y}P(x, y) \log P(x, y)$

Properity

1. Non-negativity
2. Greater than individual entropies: $H(x,y) \geq \max[H(x), H(y)]$
3. Less than the sum of individual entropies: $H(x,y) \leq H(x) + H(y)$

Conditional Entropy

The conditional entropy quantifies the amount of information needed to describe the outcome of a random variable $Y$ given that the value of another random variable $X$ is known.

$\begin{aligned} H(Y|X) &= \sum_xP(x)H(Y|X = x) \\ &= - \sum_xP(x) \sum_yP(y|x) \log P(y|x) \\ &= - \sum_{x,y}P(x,y) \log P(y|x) \end{aligned}$

Properity

1. $H(Y|X)=0$ if and only if the value of Y is completely determined by the value of X
2. $H(Y|X) = H(Y)$ if and only if Y and X are independant random variables.
3. Chain rule: Joint entropy $H(x,y) = H(x) + H(y|x) \;\; \Leftrightarrow \;\; H(y|x) = H(x, y) - H(x)$.
   Proof:

$\begin{aligned} H(x,y) &= -\sum_{x,y}P(x,y)logP(x,y) \\ &= -\sum_{x,y}P(x,y)log(P(y|x)P(x)) \\ &= -\sum_{x,y}P(x,y)logP(y|x) - \sum_{x,y}P(x,y)logP(x) \\ &= H(y|x) - \sum_{x} \sum_{y}P(x, y)logP(x) \\ &= H(y|x) - \sum_{x} logP(x)\sum_{y}P(x, y) \\ &= H(y|x) - \sum_{x} logP(x)P(x) \\ &= H(y|x) + H(x) \end{aligned}$

Cross Entropy

Cross entropy could measure of difference between 2 probability distributions p and q over the same underlying set of events.

$H(p, q) = -\sum_x p(x) \log q(x)$

Difference from joint entropy:

• Joint entropy is 2 random variables over 1 probability distribution
• Cross entropy is 1 random variable over 2 different probability distributions p, q

Cross entropy is widely used as a loss function in ML because of its relationship with KL divergence.

KL Divergence/Relative Entropy

KL divergence is the measure of how one probability distribution P is different from a second, reference probability distribution Q, or the loss you would get when you want to use p to approxmate q.

$\begin{aligned} KL(p||q) &= \sum_x p(x)\log\frac{p(x)}{q(x)} \\ &= \sum_xp(x)\log p(x) - \sum_xp(x)\log q(x) \\ &=H(p,q) - H(p) \end{aligned}$

Note:

1. $KL(p||q) \neq KL(q||p)$
2. Since KL divergence is the measure of distance between 2 probability distributions, it’s range is $[0, +\inf)$. $KL(p||q)=0$ if and only if p=q.
3. $KL(p||q)$ is converx in the pair of probability measures p,q.

Mutual Information/MI/Information Gain

Mutual information is a measure of the mutual independence between two variables. Eg: $X$ is the result of a dice, and $Y$ is whether $X$ is odd or even. So from $Y$ we could know something about $X$.

It’s defined as:

$\begin{aligned} I(X;Y) &= \sum_{x,y}p(x,y)\log \frac{p(x,y)}{p(x)p(y)} \\ &= \sum_{x,y}p(x,y)\log \frac{p(x|y)}{p(x)} =\sum_{x,y}p(x,y)\log \frac{p(y|x)}{p(y)} \end{aligned}$

Or it could be defined as:

$\begin{aligned} I(X;Y) &= \mathbb{E}_{P_{XY}}[\log \frac{P_{XY}}{P_XP_Y}] \\ &= D_{KL}(P_{XY} || P_XP_Y) \end{aligned}$

It’s also known as the information gain, which is defined as:

$\text{Info Gain}(Y,X) = H(Y) - H(Y|X)$

Performance Evaluation

Confusion Matrix

ground truth / predictions	positive	negative
positive	TP(true positive)	FN(false negative)
negative	FP(false positive)	TN(true negative)

Precision

Precision is the fraction of relevant instances among the retrieved instances, which is:

$\text{Precision} = \frac{TP}{TP + FP}$

Recall

Recall is the fraction of relevant instances that were retrieved.

$\text{Recall} = \frac{TP}{TP + FN}$

Accuracy

Accuracy is how close a given set of observations are to their true value, it treats every class equally.

$\text{Acc} = \frac{TP+TN}{TP + TN + FP + FN}$

F1

F1 is the harmonic mean of precision and recall.

$F1 = 2 * \frac{\text{Precision} * \text{Recall}}{\text{Precision} + \text{Recall}}$

$F_\beta$

F1 is the special condition of $F_\beta$, the higher $\beta$ is, the more recall is important over precision.

$F_\beta = (1+\beta^2)\frac{\text{Precision} * \text{Recall}}{\beta^2 * \text{Precision} + \text{Recall}}$

For F-score, it’s calculated based on predicted classes, instead of probabilities.

Use it for classification problems.

Support

TODO

ROC/AUC

A ROC space is defined by FPR(false positive rate) and TPR(true positive rate) as x and y axes, respectively, which depicts relative trade-offs between true positive (benefits) and false positive (costs).

FPR: defines how many incorrect positive results occur among all negative samples available during the test. Or how many negative samples that are higher than the gate are in the all negative samples.

$\text{FPR}=\frac{FP}{FP + TN}$

TPR: defines how many correct positive results occur among all positive samples available during the test. Or how many positive samples that are higher than the gate are in the all positive samples.

$\text{TPR}=\frac{TP}{TP + FN}$

How to draw ROC curve?
Use probability from the model to rank from large to small, then use the maximum prob as the gate, all samples above the gate are positive, others are negative. Change the gate and calculate the FPR(x) & TPR(y), then draw the line.

AUC is the ability of model to rank a positive sample over a negative sample

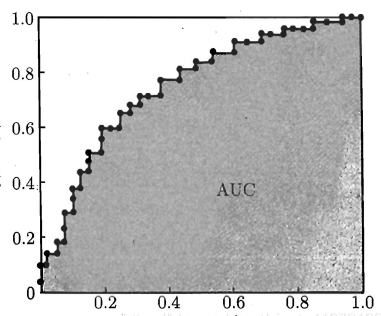AUC

Special positions

1. $(0,0)$ means classify all the samples to negative, so the FPR=0 and TPR=0
2. $(1,1)$ means classify all the samples to positive.

$\begin{aligned} x &= \text{FPR} = \frac{FP}{FP+TN} = \frac{\text{\# of Negative}}{\text{\# of Negative} + 0} = 1 \\ y &= \text{TPR} = \frac{TP}{TP+FN} = \frac{\text{\# of Positive}}{\text{\# of Positive} + 0} = 1 \\ \end{aligned}$

Use the sum of many discreate trapezoidals’ areas to approximate AUC, assume we have $N$ samples, then AUC is:

$AUC = \frac{1}{2} \sum_{i = 1}^{N - 1}(y_i + y_{i + 1})(x_{i + 1} - x_i)$

Use it for ranking problems

Advantage:

1. Don’t need to decide a gate value for positive and negative samples.
2. Not sensitive to positive and negative samples, only care about the ranking.

Disadvantage:

1. Ignore model’s ability to fit the actual probability. For example, if the model give all positive samples prob as 0.51, and all negative samples as 0.49, auc is 1, but the model is underfitted because of the cross entrophy loss is huge.
2. Not a good indicator for precision and recall. Sometimes we care only precision or recall.
3. Don’t care the ranking between positive samples and negative samples.

gAUC/group AUC

@TODO

prAUC

NDCG

Loss Function

Suitable for Classifications

Cross Entropy Loss

Cross entropy is use the estimated data distribution $p(x)$ to approximate the true data distribution $q(x)$, that is: $H(p,q)=- \sum_x p(x)\log q(x)$

So accroding to this, the cross entropy loss function is:

$L(y, \hat{y}) = -y^T \log\hat{y}$

Hinge Loss

TODO

Suitable for Regressions

Mean Square Error/MSE/L2

$L(y, \hat{y}) = \frac{1}{n} * \sum_{i = 1}^n{ (y_i - \hat{y_i} ) ^2}$

Mean Absolute Mean/MAE/L1

$L(y, \hat{y}) = \frac{1}{n} * \sum_{i = 1}^n{|y_i - \hat{y_i}|}$

Huber Loss

Huber Loss

Huber loss (green) and squared error loss (blue)

Huber loss is a combination of L1 loss and L2 loss.

$L_\delta(y, \hat{y}) = \begin{cases} \frac{1}{2} (y - \hat{y})^2, & |y - \hat{y}| \leq \delta \\ \delta|y - \hat{y}| + \frac{1}{2}\delta^2, & |y - \hat{y}| > \delta \end{cases}$

• Advantage: Optimize L1 & L2 loss’s disadvantages. (When the loss is near 0, use L2 loss. When it’s away from 0, use L1 loss.)
• Disadvantage: need to tune $\delta$.

Suitable for Classification + Regression

0-1 Loss

$l(y, \hat{y})= \begin{cases} 1, & \text{if} \; y = \hat{y} \\ 0, & \text{if} \; y \neq \hat{y} \\ \end{cases}$

• Advantage: very straightforward
• Disadvantage: discreate; derivative equals to 0, thus hard to optimize

Optimization Algorithms

Gradient Descent & its twists

Steps:

1. Determine the learning rate.
2. Initialize the parameters.
3. Choose samples for calculating the gradient of the loss functions.
4. Update the parameters.

Note: GD could gurantee the global optimal for convex functions, and local optimal for non-convex functions.

Convex Function

Batch Gradient Descent

Calculate the gradient on all the data, then update the parameters.

Stochastic Gradient Descent/SGD

Calculate the gradient based on 1 single sample, then update the parameters.

Advantage:

1. Fast, could be used for online learning
2. Loss function might fluctuate
3. Glocal optimal not guranteed (could be solved by decreasing learning rate with an appropriate rate)

Mini-batch Gradient Descent

Calculate the gradient on all the data from the batch, then update the parameters.

Usually we use $[50, 256]$ as the range for batch size, since mini-batch is very common, in most cases, the sgd in python libraries is actually mini-batch.

$\begin{aligned} w &:= w - \alpha \nabla J(\theta) \\ &= w - \frac{\alpha}{n} \sum_i^n\nabla J(\theta) \end{aligned}$

where: $\alpha$ is the learning rate, and the batch size is $n$

Note:

1. It needs to tune $alpha$ manually.
2. Global optimal not guranteed.
3. If the data is sparse, we might want to update the weights more for those frequent features, and less for those less frequent features.

Tips:

1. Shuffle the training data before using this.
2. Do batch-normalization for each mini-batch.
3. Increase learning rate when batch size increased.

TODO