Non-linear models

KNN/K-Nearest Neighbors

Key: Find k nearest neighbors of the current node, and use them to decide its class. So:

1. The definition of “near”?
2. How to decide which k should we use?
3. After we have k neighbors, what rule should we follow to decide the current node’s class?

Distance Metric

The Minkowski distance or $L_p$ distance is a metric in a normed vector space which can be considered as a generalization of other common distance metrics.

Assume variable $x$ and $y$ have dimension n, then:

$L_p(x, y) = [\sum_{i = 1}^n |x_i - y_i| ^ p]^{\frac{1}{p}}$

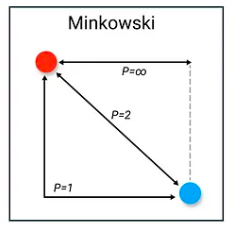Minkowski distance (src)

• When $p=1$, $L_p(x, y) = \sum_{i = 1}^n |x_i - y_i|$, which is Manhattan Distance (in 2-d, it’s the sum of the legs).
• When $p=2$, $L_p(x, y) = \sqrt{\sum_{i = 1}^n |x_i - y_i| ^ 2}$, which is Euclidean Distance (in 2-d, it’s the hypotenuse).
• When $p=\infty$, $L_p(x, y) = \max\limits_{i = 1, \dots, n}|x_i - y_i|$, which is Chebyshev Distance (the greatest of difference between two vectors along any coordinate dimension).

How to get Chebyshev distance from Minkowski distance?
TODO

Parameter K Selection

• Small K

  • If neighbors are noises, the predictions tend to be wrong.
  • The model tends to be complicated, and easy to overfit.

• Large K

  • Underfit

Usually we start with smaller k, and tune the parameter.

Classification Rule

Majority rule/The wisdom of crowds, and use 0-1 loss.

Implement: kd tree

TODO

Decision Tree

It could be seen as a set of if-else rules.

Since find the optimal decision tree is a np-complete problem, we use heuristic method for finding the sub-optimal dt.

Overall the steps are:

1. Feature selection: Find the optimal feature, split the data by this feature.
2. Build the decision tree: Repeat step1 until all the nodes are classified or we don’t have features.
3. Trim: Trim the decision tree because by step2 we might overfit.

Feature Selection

Here are some common criteria for evaluating the feature importance.

Information Gain (aka MI)

Information gain is based on entropy. Since entropy is the measure of the amount of information that data carries, information gain is the difference between two amounts of information. One is before using the current feature to split the data, one is after using the current feature.

$\text{Info Gain}(D,A) = H(D) - H(D | A)$

Here $H(D)$ is the entropy of the dataset.

Information Gain Ratio

When using information gain to choose the feature, we would naturally choose the feature with more values. So we introduce information gain ratio to solve this problem.

$g_R(D,A) = \frac{g(D,A)}{H_A(D)}$

Where $H_A(D)$ is the entropy of feature $A$ in dataset $D$. It’s similar to the way we calculate the entropy of the whole dataset, this time we only use data that has feature $A$.

$H_A(D) = -\sum_{i = 1}^{N_A} \frac{D_i}{D}log\frac{D_i}{D}$

Where $D$ is the number of samples in the dataset.

Build the Tree

ID3 algorithm
Use information gain to choose the feature when spliting data

C4.5 algorithm
Use information gain ratio to choose the feature when spliting data

Tree Trim

TODO

How to apply tree models to classification/regression problems?

TODO

Ensemble Learning

Ensemble methods use multiple algorithms to obtain better predictive performance than could be obtained from any of the constituent learning algorithms alone.

Bagging/Bootstrap aggregating

What is bootstrap dataset? A bootstrapped set is created by selecting from original training data set with replacement. Thus, a bootstrap set may contain a given example zero, one, or multiple times.
To get a bootstrap dataset, we do a sampling with replacement, so an observation may be selected more than once.

What is aggregation? Inference is done by voting of predictions of ensemble members.

• For classification problems, use the voting results. If 2 labels tied, consider adding confidence.
• For regression problems, use average, eg simple average, or weighted average with weights of base models as the average weights.

Random Forest/RF: an implementation of bagging and decision tree

Use decision tree as the base model, and add a randomness for feature selection, which is choose n features from current m candidates, and select optimal feature based on these n features.

• $n=m$: traditional decision tree
• $n=1$: randomly select 1 feature to split the data
• $n=\log_2 m$: recommended choice

Overall, random tree has 2 randomness.

• Randomness in sample selection: because of bootstrap sampling, the dataset is sampled randomly.
• Randomness in feature selection: the optimal feature is not chosen from all the features, instead it’s chosen based on randomly selected feature candidates.

Advantage

Disadvantage

Boosting

Core idea: learn a bad base model first, then keep boosting the performance until reaching a perfect standard.

Adaboost/Adaptive Boosting

Steps:

1. Calculate error rate $e_m$: the sum of classifier weights that give wrong predictions.
2. Calculate new weight $\alpha_m$: $\alpha_m = \frac{1}{2} * ln \frac{1 - e_m}{e_m}$. Note here $\alpha_m$ is inversely proportional to $e_m$.
3. Improve the boosted classifier:

$\omega_{m+1} = \begin{cases} \frac{w_{mi}}{Z_m} e^{-\alpha_m} & G_m(x_i) = y_i \\ \frac{w_{mi}}{Z_m} e^{\alpha_m} & G_m(x_i) \neq y_i \\ \end{cases}$

where $Z_m$ is a normalization factor, $Z_m=\sum_i^n w_i$

Boosting Tree

Core: Use a tree to fit residuals.

The new classifier after each iteration is:

$f_{m+1}(x) = f_m(x) + \alpha_mT(x, \Theta)$

And the loss function is:

$L(y, f_{m+1}(x)) = L(y, \;f_m(x) + \alpha_mT(x, \Theta))$

If we use MSE as the loss function, here we have:

$L(y, \;f_m(x) + \alpha_mT(x, \Theta)) = \frac{1}{2} (y - f_m(x) - \alpha_mT)^2$

Where $y - f_m(x)$ is a constant that denotes the difference between the true value and predicted value by last round classifier, which is the residual $r$, so now we have:

$\begin{aligned} L(y, \;f_m(x) + \alpha_mT(x, \Theta)) &= \frac{1}{2} (y - f_m(x) - \alpha_mT)^2 \\ &= \frac{1}{2} (r - \alpha_mT)^2 \end{aligned}$

Which means every iteration, we train a tree to fit the residual.

But boosting tree is only valid when using MSE as the loss function, so we have GBDT instead.

GBDT/Gradient Boosting Decision Tree

Use negative gradient to approximate the residual, that is:

$r_{mi} = - \left[ \frac{\partial L(y_i, f(x_i))}{\partial f(x_i)} \right]_{f(x) = f_{m-1}(x)}$

For MSE, this is the standard residual, for other loss function, this is an approximate for residuals.

Traditional Implementation
Iterate all the feature candidates, split data based on current feature, then calculate fitted residuals based on all data, $r_i = - \left[ \frac{\partial L(y_i, f(x_i))}{\partial f_{m - 1}(x_i)} \right]$. Then use loss function to calculate loss, and choose the feature with minimum loss as the feature to split the data.

So the time complexity of traditional implementation is proportional to the number of feature times the number of samples.

Regularization

Shrinkage/Learning Rate

$f_{m+1}(x) = f_m(x) + \nu \cdot \alpha_mT(x, \Theta)$

where $0 < \nu < 1$

Using small learning rates (such as $\nu < 0.1$) yields dramatic improvements in models’ generalization ability over gradient boosting without shrinking ($\nu = 1$). However, it comes at the price of increasing computational time both during training and querying: lower learning rate requires more iterations.

Stochastic Gradient Boosting Tree/SGBT
The base model should be trained on bootstraped datasets. Use $f$ to denote the size of training set.

• $f=1$: same as gradient boosting
• $0.5 \leq f \leq 0.8$: recommended interval
• $f=0.5$: most common choice

Number of Observations in Leaves
Limiting the minimum number of observations in trees’ terminal nodes.
Penalize Complexity of Tree
$L_2$ penality on the leaf values.

XGBoost/eXtreme Gradient Boosting

Xgboost is modified based on gbdt, where it added regularization and use a second order taylor series to get a more precise loss function.

Taylor series of $f(x)$ on $x=a$ is below:

$f(x)|_{x=a} = f(a) + \frac{f'(a)}{1!}(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \frac{f'''(a)}{3!}(x - a)^3 + \dots$

Assume the size of samples is $n$, then the loss function is:

$\begin{aligned} Loss(y, \hat y) &= \sum_{i = 1}^n {L[y_i, f_m(x_i)] + \Omega(T_m)} \\ &= \sum_{i = 1}^n {L[y_i, f_{m-1}(x_i) + T_m(x_i)] + \Omega(T_m)} \\ \end{aligned}$

where $T_m$ are all the trees.

To simplify the process, we only use 1 sample, then use a second taylor series at $f_{m-1}(x_i)$, we have:

$\begin{aligned} L[y_i, f_{m-1}(x_i) + T_t(x_i)] &= L(y_i, f_{m-1}(x_i)) + \frac{\partial{L(y_i, f_{m-1}(x_i))}}{\partial{f_{m-1}}} * T_m(x_i) + \frac{1}{2} \frac{\partial{L^2(y_i, f_{m-1}(x_i))}}{\partial{f_{m-1}^2(x_i)}} * T_m^2(x_i) \\ &= L(y_i, f_{m-1}(x_i)) + g(f_{m-1}(x_i)) * T_m(x_i) + \frac{1}{2} h(f_{m-1}(x_i)) * T_m^2(x_i) \\ &= L(y_i, f_{m-1}(x_i)) + g_i * T_m(x_i) + \frac{1}{2} h_i * T_m^2(x_i) \end{aligned}$

Use this result to $Loss(y, \hat y)$, now we have:

$\begin{aligned} Loss(y, \hat y) &= \sum_{i = 1}^n {L[y_i, f_{m-1}(x_i) + T_m(x_i)] + \Omega(T_m)} \\ &= \sum_{i = 1}^n { \{ L[y_i, f_{m-1}(x_i)] + g_i * T_m(x_i) + \frac{1}{2} h_i * T_m^2(x_i) \}+ \Omega(T_m)} \\ &= \sum_{i = 1}^n { \{ L[y_i, f_{m-1}(x_i)] + g_i * T_m(x_i) + \frac{1}{2} h_i * T_m^2(x_i) \}+ \gamma |T| + \frac{1}{2} \lambda \sum_{j = 1}^T | w_j |^2} \end{aligned}$

Note:

1. $T$ is the number of leaves at iteration m
2. $w_j$ is the weight of leaf j

Since:

• $L[y_i, f_{m-1}(x_i)]$ and $\gamma |T|$ are both constants, we could just ignore them
• $T_m(x)$ is the sum of leaf weights at iteration m, so:

$\begin{aligned} \sum_{i = 1}^n g_i * T_m(x) &= \sum_{j = 1}^T w_j * (\sum_{i \in I_j}g_i)\\ \sum_{i = 1}^n \frac{1}{2} h_i * T_m^2(x) &= \frac{1}{2} \sum_{j = 1}^T w_j^2 * (\sum_{i \in I_j}h_i) \end{aligned}$

where $I_j$ denotes all the samples that fall in leaf j

Now we have loss function as:

$\begin{aligned} Loss(y, \hat y) &= \sum_{i = 1}^n { \{ L[y_i, f_{m-1}(x_i)] + g_i * T_m(x_i) + \frac{1}{2} h_i * T_m^2(x_i) \}+ \gamma |T| + \frac{1}{2} \lambda \sum_{j = 1}^T | w_j |^2} \\ &= \sum_{i = 1}^n { [g_i * T_m(x_i) + \frac{1}{2} h_i * T_m^2(x_i)] + \frac{1}{2} \lambda \sum_{j = 1}^T {|w_j|^2}} \\ &= \sum_{j = 1}^T [(\sum_{i \in I_j}g_i)w_j + \frac{1}{2}(\sum_{i \in I_j}h_i + \lambda)w_j^2] \end{aligned}$

Calculate the derivative of loss function of $w$, then we have:

$\begin{aligned} \frac{\partial L}{\partial {w}} &= \sum{g} + (\sum{h} + \lambda) w \end{aligned}$

Let derivative = 0, then we have optimal $w$:

$\begin{aligned} w^* = -\frac{\sum{g}}{\sum{h} + \lambda} \end{aligned}$

Then the minimum loss (with constants) is:

$\begin{aligned} Loss(y, \hat y) &= - \frac{1}{2} \sum_{j = 1}^T {[\frac{(\sum{g})^2}{\sum{h} + \lambda}] + \gamma |T|} \end{aligned}$

From the loss function formula we know the loss is related to the structure of the tree ($T$ in the equation). So in order to find the minimum loss, we need to iterate all different structured trees, which is too time-consuming.

Consider a heuristic method, start with a single node, and then find the next feature to split the data. The criteria for selecting feature is, after spliting by this feature, the loss would decrease.
Loss reduction:

$\begin{aligned} \text{Loss Reduction} &= L_{\text{no split}} - (L_{\text{left nodes after spliting}} + L_{\text{right nodes after spliting}}) \\ &= - \frac{1}{2} [\frac{(\sum {g_n})^2}{\sum {h_n} + \lambda} - \frac{(\sum {g_l})^2}{\sum {h_l} + \lambda} - \frac{(\sum {g_r})^2}{\sum {h_r} + \lambda}] + \gamma (1 - 1 - 1) \\ \\ &= \frac{1}{2} [\frac{(\sum {g_l)^2}}{\sum {h_l} + \lambda} + \frac{(\sum {g_r})^2}{\sum {h_r} + \lambda} - \frac{(\sum {g_n})^2}{\sum {h_n} + \lambda} ] - \gamma \end{aligned}$

Tree generation based on pre-sorted features

If loss reduction > 0, then this feature should split the data, else we should prune. So everytime we find the maximum loss reduction to split the data.

To speed up the spliting, we calculate the feature reduction first:

$\text{Loss Reduction} = L_{\text{no split}} - (L_{\text{left nodes after spliting}} + L_{\text{right nodes after spliting}})$

and then sort them from largest to smallest.

Pros: fast speed, could run in parallel.
Cons:

1. Need to iterate all the data to calculate loss reduction
2. Need to store the sorted results

Note: Even xgb could run in parallel, it’s parallel in feature level, not in data level.

LightGBM

TODO