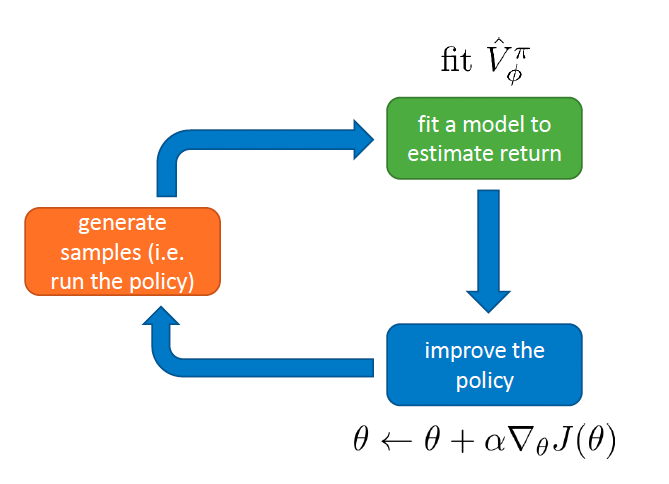
sample { s i , a i } \{ s_i, a_i \} { s i , a i } π θ ( a ∣ s ) \pi_\theta(a|s) π θ ( a ∣ s )
fit V ^ ϕ ( s ) \hat{V}_\phi(s) V ^ ϕ ( s ) { ( s i , t , r ( s i , t , a i , t ) + model ( s i , t + 1 ) ⏟ y i , t ) } \{ (s_{i, t}, \underbrace{r(s_{i,t}, a_{i,t}) + \text{model}(s_{i,t+1})}_{y_{i,t}}) \} { ( s i , t , y i , t r ( s i , t , a i , t ) + model ( s i , t + 1 ) ) }
evaluate A ^ π ( s i , a i ) = r ( s i , a i ) + γ V ^ ϕ π ( s i ′ ) − V ^ ϕ π ( s i ) \hat{A}^\pi(s_i, a_i) = r(s_i, a_i) + \gamma \hat{V}^\pi_\phi(s'_i) - \hat{V}^\pi_\phi(s_i) A ^ π ( s i , a i ) = r ( s i , a i ) + γ V ^ ϕ π ( s i ′ ) − V ^ ϕ π ( s i )
∇ θ J ( θ ) ≈ 1 N ∑ i ∇ θ log π θ ( a i ∣ s i ) A ^ π ( s i , a i ) \nabla_\theta J(\theta) \approx \frac{1}{N}\sum_i \nabla_\theta \log \pi_\theta(a_i | s_i) \hat{A}^\pi(s_i, a_i) ∇ θ J ( θ ) ≈ N 1 ∑ i ∇ θ log π θ ( a i ∣ s i ) A ^ π ( s i , a i ) θ ← θ + α ∇ θ J ( θ ) \theta \leftarrow \theta + \alpha \nabla_\theta J(\theta) θ ← θ + α ∇ θ J ( θ )
target function:
∇ θ J ( θ ) ≈ 1 N ∑ i = 1 N ∑ t = 1 T ∇ θ log π θ ( a i , t ∣ s i , t ) Q ^ i , t \begin{aligned}
\nabla_\theta J(\theta) \approx \frac{1}{N}\sum_{i = 1}^N \sum_{t=1}^T \nabla_\theta \log \pi_\theta(a_{i,t} | s_{i,t}) \hat{Q}_{i,t}
\end{aligned} ∇ θ J ( θ ) ≈ N 1 i = 1 ∑ N t = 1 ∑ T ∇ θ log π θ ( a i , t ∣ s i , t ) Q ^ i , t
notes: Q ^ i , t \hat{Q}_{i,t} Q ^ i , t a i , t a_{i,t} a i , t s i , t s_{i,t} s i , t
Q ^ i , t ≈ ∑ t ′ = t T r ( s i , t , a i , t ) \hat{Q}_{i,t} \approx \sum_{t' = t}^Tr(s_{i,t}, a_{i,t})
Q ^ i , t ≈ t ′ = t ∑ T r ( s i , t , a i , t )
A better estimate rather than a single one will be:
Q ^ i , t ≈ ∑ t ′ = t T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ] \hat{Q}_{i,t} \approx \sum_{t' = t}^TE_{\pi_\theta}[r(s_{t'}, a_{t'})|s_t, a_t]
Q ^ i , t ≈ t ′ = t ∑ T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ]
Use expected estimates Q ^ i , t \hat{Q}_{i,t} Q ^ i , t
To futher reduce variance, reduce a baseline from Q. This baseline could be the expected value of Q(use average to approximate):
b t = 1 N ∑ i Q ( s i , t , a i , t ) b_t = \frac{1}{N}\sum_iQ(s_{i,t}, a_{i,t})
b t = N 1 i ∑ Q ( s i , t , a i , t )
So the target function will be:
∇ θ J ( θ ) ≈ 1 N ∑ i = 1 N ∑ t = 1 T ∇ θ log π θ ( a i , t ∣ s i , t ) Q ^ i , t ≈ 1 N ∑ i = 1 N ∑ t = 1 T ∇ θ log π θ ( a i , t ∣ s i , t ) ( ∑ t ′ = 1 T r ( s i , t ′ , a i , t ′ ) − b ) \begin{aligned}
\nabla_\theta J(\theta) &\approx \frac{1}{N}\sum_{i = 1}^N \sum_{t=1}^T \nabla_\theta \log \pi_\theta(a_{i,t} | s_{i,t}) \hat{Q}_{i,t} \\
&\approx \frac{1}{N}\sum_{i = 1}^N \sum_{t=1}^T \nabla_\theta \log \pi_\theta(a_{i,t} | s_{i,t}) \Big( \sum_{t'=1}^Tr(s_{i, t'}, a_{i, t'}) - b \Big)
\end{aligned} ∇ θ J ( θ ) ≈ N 1 i = 1 ∑ N t = 1 ∑ T ∇ θ log π θ ( a i , t ∣ s i , t ) Q ^ i , t ≈ N 1 i = 1 ∑ N t = 1 ∑ T ∇ θ log π θ ( a i , t ∣ s i , t ) ( t ′ = 1 ∑ T r ( s i , t ′ , a i , t ′ ) − b )
Because policy gradient calculates on every single sample, it’s unbiased but has high vairance.
To deal with this high variance, we introduce Actor-Critic.
Consider state-action value function, that is total reward from taking a t a_t a t s t s_t s t
Q π ( s t , a t ) = ∑ t ′ = t T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ] Q^\pi(s_t, a_t) = \sum_{t' = t}^TE_{\pi_\theta}[r(s_{t'}, a_{t'})|s_t, a_t]
Q π ( s t , a t ) = t ′ = t ∑ T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ]
Consider state value function, that is average rewards from s t s_t s t
V π ( s t ) = E a t ∼ π θ ( a t ∣ s t ) [ Q π ( s t , a t ) ] V^\pi(s_t) = E_{a_t \sim \pi_\theta(a_t|s_t)}[Q^\pi(s_t, a_t)]
V π ( s t ) = E a t ∼ π θ ( a t ∣ s t ) [ Q π ( s t , a t ) ]
In this way we could use A π A^\pi A π a t a_t a t π \pi π
A π ( s t , a t ) = Q π ( s t , a t ) − V π ( s t ) A^\pi(s_t, a_t) = Q^\pi(s_t, a_t) - V^\pi(s_t)
A π ( s t , a t ) = Q π ( s t , a t ) − V π ( s t )
And the target function will be:
∇ θ J ( θ ) ≈ 1 N ∑ i = 1 N ∑ t = 1 T ∇ θ log π θ ( a i , t ∣ s i , t ) Q ^ i , t ≈ 1 N ∑ i = 1 N ∑ t = 1 T ∇ θ log π θ ( a i , t ∣ s i , t ) A π ( s i , t , a i , t ) \begin{aligned}
\nabla_\theta J(\theta) &\approx \frac{1}{N}\sum_{i = 1}^N \sum_{t=1}^T \nabla_\theta \log \pi_\theta(a_{i,t} | s_{i,t}) \hat{Q}_{i,t} \\
&\approx \frac{1}{N}\sum_{i = 1}^N \sum_{t=1}^T \nabla_\theta \log \pi_\theta(a_{i,t} | s_{i,t}) A^\pi(s_{i,t}, a_{i,t})
\end{aligned} ∇ θ J ( θ ) ≈ N 1 i = 1 ∑ N t = 1 ∑ T ∇ θ log π θ ( a i , t ∣ s i , t ) Q ^ i , t ≈ N 1 i = 1 ∑ N t = 1 ∑ T ∇ θ log π θ ( a i , t ∣ s i , t ) A π ( s i , t , a i , t )
We now have 3 options to optimize: Q , V , A Q,V,A Q , V , A
For Q Q Q
Q π ( s t , a t ) = ∑ t ′ = t T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ] = r ( s t , a t ) + ∑ t ′ = t + 1 T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ] = r ( s t , a t ) + E s t + 1 ∼ p ( s t + 1 ∣ s t , a t ) [ V π ( s t + 1 ) ] ≈ r ( s t , a t ) + V π ( s t + 1 ) \begin{aligned}
Q^\pi(s_t, a_t) &= \sum_{t' = t}^TE_{\pi_\theta}[r(s_{t'}, a_{t'})|s_t, a_t] \\
&= r(s_t, a_t) + \sum_{t' = t+1}^TE_{\pi_\theta}[r(s_{t'}, a_{t'})|s_t, a_t] \\
&= r(s_t, a_t) + E_{s_{t+1} \sim p(s_{t+1}|s_t, a_t)}[V^\pi(s_{t+1})] \\
&\approx r(s_t, a_t) + V^\pi(s_{t+1})
\end{aligned} Q π ( s t , a t ) = t ′ = t ∑ T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ] = r ( s t , a t ) + t ′ = t + 1 ∑ T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ] = r ( s t , a t ) + E s t + 1 ∼ p ( s t + 1 ∣ s t , a t ) [ V π ( s t + 1 ) ] ≈ r ( s t , a t ) + V π ( s t + 1 )
Then we get:
A π ( s t , a t ) = Q π ( s t , a t ) − V π ( s t ) ≈ r ( s t , a t ) + V π ( s t + 1 ) − V π ( s t ) \begin{aligned}
A^\pi(s_t, a_t) &= Q^\pi(s_t, a_t) - V^\pi(s_t) \\
&\approx r(s_t, a_t) + V^\pi(s_{t+1}) - V^\pi(s_t)
\end{aligned} A π ( s t , a t ) = Q π ( s t , a t ) − V π ( s t ) ≈ r ( s t , a t ) + V π ( s t + 1 ) − V π ( s t )
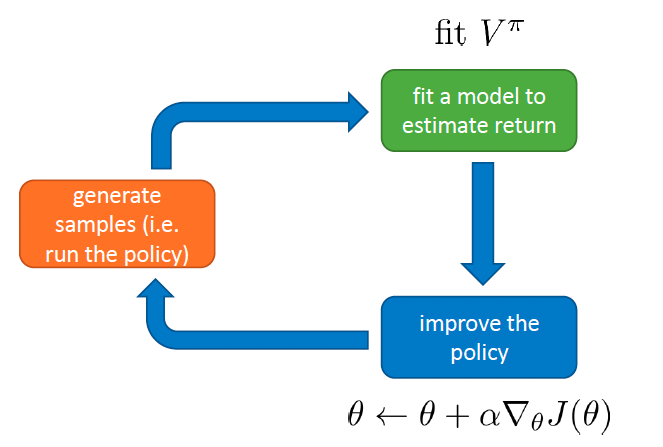
So we choose to fit V π ( s ) V^\pi(s) V π ( s )
V π ( s ) V^\pi(s) V π ( s )
To perform optimization, like what the policy gradient does, we could use monte-carlo to get the estimated expected value:
V π ( s t ) = E a t ∼ π θ ( a t ∣ s t ) [ Q π ( s t , a t ) ] ≈ ∑ t ′ = t T r ( s t ′ , a t ′ ) ≈ 1 N ∑ n = 1 N ∑ t ′ = t T r ( s t ′ , a t ′ ) \begin{aligned}
V^\pi(s_t) &= E_{a_t \sim \pi_\theta(a_t|s_t)}[Q^\pi(s_t, a_t)] \\
&\approx \sum_{t'=t}^Tr(s_{t'}, a_{t'}) \\
&\approx \frac{1}{N}\sum_{n=1}^N\sum_{t'=t}^Tr(s_{t'}, a_{t'})
\end{aligned} V π ( s t ) = E a t ∼ π θ ( a t ∣ s t ) [ Q π ( s t , a t ) ] ≈ t ′ = t ∑ T r ( s t ′ , a t ′ ) ≈ N 1 n = 1 ∑ N t ′ = t ∑ T r ( s t ′ , a t ′ )
Ideally, we need to collect all possible trajectories from s t ′ s_{t'} s t ′
But if we use a neural network to fit V π ( s t ) V^\pi(s_t) V π ( s t ) in a single trajectory , it will generalize to all trajectories (generation in ML).
training set: { ( s i , t , V π ( s t ) ≈ 1 N ∑ n = 1 N ∑ t ′ = t T r ( s t ′ , a t ′ ) ⏟ y i , t ) } \{ (s_{i, t}, \underbrace{V^\pi(s_t) \approx \frac{1}{N}\sum_{n=1}^N\sum_{t'=t}^Tr(s_{t'}, a_{t'})}_{y_{i,t}} ) \} { ( s i , t , y i , t V π ( s t ) ≈ N 1 n = 1 ∑ N t ′ = t ∑ T r ( s t ′ , a t ′ ) ) } y i , t y_{i,t} y i , t y i , t y_{i,t} y i , t
y i , t = V π ( s t ) = ∑ t ′ = t T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ] ≈ r ( s t , a t ) + ∑ t ′ = t + 1 T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ] = r ( s t , a t ) + E s t + 1 ∼ p ( s t + 1 ∣ s t , a t ) [ V π ( s t + 1 ) ] ≈ r ( s t , a t ) + V π ( s t + 1 ) \begin{aligned}
y_{i,t} &= V^\pi(s_t) \\
&= \sum_{t' = t}^TE_{\pi_\theta}[r(s_{t'}, a_{t'})|s_t, a_t] \\
&\approx r(s_t, a_t) + \sum_{t' = t+1}^TE_{\pi_\theta}[r(s_{t'}, a_{t'})|s_t, a_t] \\
&= r(s_t, a_t) + E_{s_{t+1} \sim p(s_{t+1}|s_t, a_t)}[V^\pi(s_{t+1})] \\
&\approx r(s_t, a_t) + V^\pi(s_{t+1})
\end{aligned} y i , t = V π ( s t ) = t ′ = t ∑ T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ] ≈ r ( s t , a t ) + t ′ = t + 1 ∑ T E π θ [ r ( s t ′ , a t ′ ) ∣ s t , a t ] = r ( s t , a t ) + E s t + 1 ∼ p ( s t + 1 ∣ s t , a t ) [ V π ( s t + 1 ) ] ≈ r ( s t , a t ) + V π ( s t + 1 )
Since we don’t know V π ( s t + 1 ) V^\pi(s_{t+1}) V π ( s t + 1 ) V ^ ( s t + 1 ) \hat{V}(s_{t+1}) V ^ ( s t + 1 )
Thus the training set is: { ( s i , t , r ( s i , t , a i , t ) + V ^ ϕ π ( s i , t + 1 ) ⏟ y i , t ) } \{ (s_{i, t}, \underbrace{r(s_{i,t}, a_{i,t}) + \hat{V}^\pi_\phi(s_{i,t+1})}_{y_{i,t}}) \} { ( s i , t , y i , t r ( s i , t , a i , t ) + V ^ ϕ π ( s i , t + 1 ) ) }
Use supervised regression loss to optimize:
L ( ϕ ) = 1 2 ∑ i ∣ ∣ V ^ ϕ π ( s i ) − y i ∣ ∣ 2 \mathcal{L}(\phi) = \frac{1}{2}\sum_i || \hat{V}^\pi_\phi(s_i) - y_i ||^2
L ( ϕ ) = 2 1 i ∑ ∣ ∣ V ^ ϕ π ( s i ) − y i ∣ ∣ 2
This “bootstrapped” estimate has lower variance because it’s using V ^ ϕ π ( s i ) \hat{V}^\pi_\phi(s_i) V ^ ϕ π ( s i ) V ^ ϕ π ( s i ) \hat{V}^\pi_\phi(s_i) V ^ ϕ π ( s i )
If T (episode length) is ∞ \infin ∞ V ^ ϕ π ( s i ) \hat{V}^\pi_\phi(s_i) V ^ ϕ π ( s i ) y i , t y_{i,t} y i , t
y i , t = r ( s i , t , a i , t ) + γ V ^ ϕ π ( s i , t + 1 ) y_{i,t} = r(s_{i,t}, a_{i,t}) + \gamma \hat{V}^\pi_\phi(s_{i,t+1})
y i , t = r ( s i , t , a i , t ) + γ V ^ ϕ π ( s i , t + 1 )
batch actor-critic algorithm (with discount factor):
sample { s i , a i } \{ s_i, a_i \} { s i , a i } π θ ( a ∣ s ) \pi_\theta(a|s) π θ ( a ∣ s )
fit V ^ ϕ ( s ) \hat{V}_\phi(s) V ^ ϕ ( s )
evaluate A ^ π ( s i , a i ) = r ( s i , a i ) + γ V ^ ϕ π ( s i ′ ) − V ^ ϕ π ( s i ) \hat{A}^\pi(s_i, a_i) = r(s_i, a_i) + \gamma \hat{V}^\pi_\phi(s'_i) - \hat{V}^\pi_\phi(s_i) A ^ π ( s i , a i ) = r ( s i , a i ) + γ V ^ ϕ π ( s i ′ ) − V ^ ϕ π ( s i )
∇ θ J ( θ ) ≈ 1 N ∑ i ∇ θ log π θ ( a i ∣ s i ) A ^ π ( s i , a i ) \nabla_\theta J(\theta) \approx \frac{1}{N}\sum_i \nabla_\theta \log \pi_\theta(a_i | s_i) \hat{A}^\pi(s_i, a_i) ∇ θ J ( θ ) ≈ N 1 ∑ i ∇ θ log π θ ( a i ∣ s i ) A ^ π ( s i , a i ) θ ← θ + α ∇ θ J ( θ ) \theta \leftarrow \theta + \alpha \nabla_\theta J(\theta) θ ← θ + α ∇ θ J ( θ )
online actor-critic:
take action a ∼ π θ ( a ∣ s ) a \sim \pi_\theta(a|s) a ∼ π θ ( a ∣ s ) ( s , a , s ′ , r ) (s, a, s', r) ( s , a , s ′ , r ) R \mathcal{R} R
sample a batch { s i , a i , r i , s i ′ } \{s_i, a_i, r_i, s_i'\} { s i , a i , r i , s i ′ } R \mathcal{R} R
update Q ^ ϕ π \hat{Q}^\pi_\phi Q ^ ϕ π y i = r i + γ Q ^ ϕ π ( s i ′ , a i ′ ) , ∀ s i , a i y_i = r_i + \gamma \hat{Q}^\pi_\phi(s_i',a_i'), \forall s_i, a_i y i = r i + γ Q ^ ϕ π ( s i ′ , a i ′ ) , ∀ s i , a i
∇ θ J ( θ ) ≈ 1 N ∑ i ∇ θ log π θ ( a ∣ s ) Q ^ π ( s i , a i π ) \nabla_\theta J(\theta) \approx \frac{1}{N}\sum_i \nabla_\theta \log \pi_\theta(a | s) \hat{Q}^\pi(s_i, a_i^\pi) ∇ θ J ( θ ) ≈ N 1 ∑ i ∇ θ log π θ ( a ∣ s ) Q ^ π ( s i , a i π ) θ ← θ + α ∇ θ J ( θ ) \theta \leftarrow \theta + \alpha \nabla_\theta J(\theta) θ ← θ + α ∇ θ J ( θ )
In online actor-critic, we need to fit Q ( s , a ) Q(s,a) Q ( s , a ) V ( s ) V(s) V ( s ) y i y_i y i
Two separate networks for actor and critic
Or we could train a shared bottom with two different heads.
In deep learning we usually update V ^ ϕ π ← r + γ V ^ ϕ π ( s ′ ) \hat{V}^\pi_\phi \leftarrow r + \gamma \hat{V}^\pi_\phi(s') V ^ ϕ π ← r + γ V ^ ϕ π ( s ′ )
synchronized parallel actor-critic n simulators if the batch size is n
asynchronous parallel actor-critic
use replay buffer
Actually we could see actor-critic as calculating A ^ π ( s i , a i ) = r ( s i , a i ) + γ V ^ ϕ π ( s i ′ ) − V ^ ϕ π ( s i ) \hat{A}^\pi(s_i, a_i) = r(s_i, a_i) + \gamma \hat{V}^\pi_\phi(s'_i) - \hat{V}^\pi_\phi(s_i) A ^ π ( s i , a i ) = r ( s i , a i ) + γ V ^ ϕ π ( s i ′ ) − V ^ ϕ π ( s i ) A ^ π ( s i , a i ) = ∑ t ′ = t T γ t ′ − t r ( s i , t ′ , a i , t ′ ) − V ^ ϕ π ( s i , t ) \hat{A}^\pi(s_i, a_i)=\sum_{t' = t}^T \gamma^{t'-t}r(s_{i,t'}, a_{i, t'}) - \hat{V}^\pi_\phi(s_{i,t}) A ^ π ( s i , a i ) = ∑ t ′ = t T γ t ′ − t r ( s i , t ′ , a i , t ′ ) − V ^ ϕ π ( s i , t )
As we mentioned above, actor-critic has lower variance but high bias (if the estimated value is wrong, which is very common), while policy gradient has no bias but high variance (because it estimates on every single sample).
So maybe we could find a point between these two, using rewards from some steps to calculate A ^ π ( s i , a i ) \hat{A}^\pi(s_i, a_i) A ^ π ( s i , a i )
A ^ π ( s t , a t ) = ∑ t ′ = t t + n γ t ′ − t r ( s t ′ , a t ′ ) − V ^ ϕ π ( s t ) + γ n V ^ ϕ π ( s t + n ) \hat{A}^\pi(s_t, a_t) = \sum_{t' = t}^{t+n} \gamma^{t'-t}r(s_{t'}, a_{t'}) - \hat{V}^\pi_\phi(s_{t}) + \gamma^n \hat{V}^\pi_\phi(s_{t+n})
A ^ π ( s t , a t ) = t ′ = t ∑ t + n γ t ′ − t r ( s t ′ , a t ′ ) − V ^ ϕ π ( s t ) + γ n V ^ ϕ π ( s t + n )
Moreover, we could use attention-like mechanism to get a weighted combination of n-step returns:
A ^ G A E π ( s t , a t ) = ∑ n = 1 ∞ w n A ^ n π ( s t , a t ) = ∑ t ′ = t ∞ ( γ λ ) t ′ − t ( r ( s i , a i ) + γ V ^ ϕ π ( s i ′ ) − V ^ ϕ π ( s i ) ) ⏟ δ t ′ \begin{aligned}
\hat{A}^\pi_{GAE}(s_t, a_t) &= \sum_{n=1}^\infin w_n \hat{A}^\pi_n(s_t, a_t) \\
&= \sum_{t'=t}^\infin (\gamma \lambda)^{t'-t} \underbrace{\Big(r(s_i, a_i) + \gamma \hat{V}^\pi_\phi(s'_i) - \hat{V}^\pi_\phi(s_i)\Big)}_{\delta_{t'}}
\end{aligned} A ^ G A E π ( s t , a t ) = n = 1 ∑ ∞ w n A ^ n π ( s t , a t ) = t ′ = t ∑ ∞ ( γ λ ) t ′ − t δ t ′ ( r ( s i , a i ) + γ V ^ ϕ π ( s i ′ ) − V ^ ϕ π ( s i ) )
The γ λ \gamma \lambda γ λ
实现思路很简单,用actor_net,输入state,输出action。用critic_net,输入state,输出dim=1的值(value)。